Cho nửa đường tròn đường kính $AB = 2R.$ Từ $A$ và $B$ kẻ hai tiếp tuyến $Ax,\,By.$ Trên $Ax$ lấy điểm $M$ rồi kẻ tiếp tuyến $MP$ cắt $By$ tại $N.$Khi đó tỉ số $\dfrac{{{S_{MON}}}}{{{S_{APB}}}}$ trong trường hợp $AM = \dfrac{R}{2}$ là:

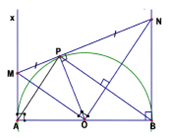
Theo tính chất hai tiếp tuyến cắt nhau ta có

$OM$ là tia phân giác của góc $\widehat {AOP}$ và $ON$ là tia phân giác của góc $\widehat {BOP}.$ Do đó $\widehat {MOA} = \widehat {MOP},\,\,\widehat {PON} = \widehat {BON}\,\,\left( 1 \right).$

Ta lại có $\widehat {AOP},\,\widehat {BOP}$ là hai góc kề bù nên $\widehat {AOP} + \,\widehat {BOP} = {180^0}\,\,\left( 2 \right).$

Từ $\left( 1 \right)$ và $\left( 2 \right)$ ta suy ra

$\widehat {MON} = \widehat {MOP} + \widetilde {PON} = \dfrac{1}{2}\left( {\widehat {AOM} + \widehat {MOP} + \widehat {PON} + \widehat {NOB}} \right)$

$= \dfrac{1}{2}\left( {\widehat {AOP} + \widehat {POB}} \right) = \dfrac{1}{2}{.180^0} = {90^0}\,\,.$

Nên tam giác $MON$ là tam giác vuông tại $O$ có $OP \bot MN$ ($OP$ là tiếp tuyến).

Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông $MON$ ta có $O{P^2} = PN.PM.$

Ta lại có $OP = R,\,AM = PM,\,BN = NP$ (tính chất hai tiếp tuyến cắt nhau).

Do đó $AM.BN = {R^2}.$

hay $PN.PM = {R^2}$

Mà $PM = AM = \dfrac{R}{2} \Rightarrow PM = \dfrac{R}{2} \Rightarrow PN = 2R.$

Do đó $MN = PM + PN = \dfrac{R}{2} + 2R = \dfrac{{5R}}{2} \Rightarrow \dfrac{{MN}}{{AB}} = \dfrac{{\dfrac{{5R}}{2}}}{{2R}} = \dfrac{5}{4}$

Ta có có $\widehat {APB}$ là góc nội tiếp chắn nửa đường tròn nên $\widehat {APB} = {90^0}\,\,\left( 4 \right).$

Theo tính chất hai tiếp tuyến ta có

$NB \bot ON \Rightarrow \widehat {OBN} = {90^0},\,\,NP \bot OP \Rightarrow \widehat {OPN} = {90^0} \Rightarrow \widehat {OBN} + \widehat {OPN} = {180^0}.$

Do đó tứ giác $OBNP$ là tứ giác nội tiếp. Từ đó $\widehat {OBP} = \widehat {PNO}\,\,\left( 5 \right).$

Từ $\,\left( 4 \right)$; $\left( 5 \right)$ và $\widehat {MON} = 90^\circ$ suy ra hai tam giác vuông $APB$ và $MON$ đồng dạng với nhau.

Suy ra  $\dfrac{{{S_{MON}}}}{{{S_{APB}}}} = {\left( {\dfrac{{MN}}{{AB}}} \right)^2} = {\left( {\dfrac{5}{4}} \right)^2} = \dfrac{{25}}{{16}}.$