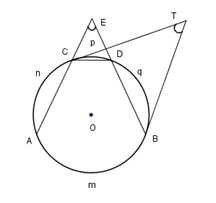
Cho hình vẽ ở bên. Giả sử rằng số đo các cung

\(AnC,CpD,DqB\) lần lượt có số đo là \(\alpha ,\beta ,\,\alpha \,\,\left( {2\alpha  + \beta  < {{360}^0}} \right).\)                       

Khi đó

Theo giả thiết ta có \(sđ\,\overparen{AmB} = {360^0} - \left( {sđ\,\overparen{AnC} + sđ\,\overparen{CpD} + sđ\,\overparen{DqB}} \right) = {360^0} - \left( {2\alpha  + \beta } \right)\,\,\left( {\,1} \right).\)

Theo tính chất góc có đỉnh nằm bên ngoài của đường tròn và áp dụng \(\left( 1 \right)\) ta có

\(\widehat {CED} = \dfrac{1}{2}\left( {sđ\,\overparen{AmB}\, - sđ\,\overparen{CpD}} \right) = \dfrac{1}{2}\left( {{{360}^0} - 2\alpha  - \beta  - \beta } \right) = {180^0} - \alpha  - \beta \,\,\left( 2 \right).\)

Ta cũng có \(\widehat {BTC}\) là góc có đỉnh ở ngoài đường tròn ( có hai cạnh đều là tiếp tuyến của đường tròn) nên

 $\widehat {BTC} = \dfrac{1}{2}\left( {sđ\,\overparen{CAB} - sđ\,\overparen{CDB}} \right) = \dfrac{1}{2}\left[ {\left( {sđ\,\overparen{AmB} + sđ\,\overparen{AnC}} \right) - \left( {sđ\,\overparen{CpD} + sđ\,\overparen{DqB}} \right)} \right]$

$ = \dfrac{1}{2}\left[ {\left\{ {\left( {{{360}^0} - 2\alpha  - \beta } \right) + \alpha } \right\} - \left( {\beta  + \alpha } \right)} \right]$

${\kern 1pt}  = \dfrac{1}{2}\left( {{{360}^0} - 2\alpha  - 2\beta } \right) = {180^0} - \alpha  - \beta \,\,\left( 3 \right).$

Từ \(\left( 2 \right)\) và \((3)\) ta suy ra \(\widehat {CED} = \widehat {BTC}.\)