Câu hỏi:
2 năm trước
Cho \(\Delta ABC\) nội tiếp đường tròn \(\left( {O;R} \right)\)có độ dài các cạnh là \(AB = c,\,BC = a,\,CA = b\) kẻ \(AH \bot BC,\,\,AO\) cắt \(\left( O \right)\) tại \(D.\) Diện tích \(S\) của \(\Delta ABC\) là:
Trả lời bởi giáo viên
Đáp án đúng: a
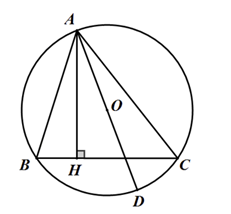
Xét \(\Delta ABH\) và \(\Delta ADC\)có \(\widehat {AHB} = \widehat {ACD} = {90^0}.\)
Các góc \(\widehat {ABC},\widehat {ADC}\) là các góc nội tiếp cùng chắn cung \(AC\) nên \(\widehat {ABC} = \widehat {ADC}.\)
Do đó \(\Delta ABH \backsim \Delta ADC.\)
Vì vậy \(\dfrac{{AB}}{{AD}} = \dfrac{{AH}}{{AC}} \Rightarrow AH = \dfrac{{AB.AC}}{{AD}} = \dfrac{{bc}}{{2R}}.\)
Diện tích tam giác \(ABC\) là:
\(S = \dfrac{1}{2}AH.BC = \dfrac{1}{2}\left( {\dfrac{{bc}}{{2R}}} \right).a = \dfrac{{abc}}{{4R}}.\)
Hướng dẫn giải:
Tính \(AH\) dựa vào tính chất tam giác đồng dạng từ đó tính diện tích tam giác \(ABC\) .
