Câu hỏi:
2 năm trước
Cho nửa đường tròn đường kính \(AB = 2R.\) Từ \(A\) và \(B\) kẻ hai tiếp tuyến \(Ax\) và \(By.\) Qua điểm \(M\) thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến \(Ax,\,By\) lần lượt tại \(C\) và \(D.\) Khi đó độ dài \(AC + BD\) nhỏ nhất khi:
Trả lời bởi giáo viên
Đáp án đúng: d
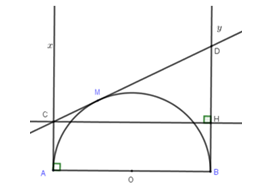
Do \(CM,\,DM\) là các tiếp tuyến nên ta có \(MD = BD,\,\,CM = CA.\)
Từ đó \(CA + BD = CM + MD = CD.\)
Từ \(C\) hạ đường cao \(CH\) xuống \(BD.\)
Khi đó \(\Delta HCD\) vuông tại \(H,\) có \(CD\) là cạnh huyền và \(CH\) là cạnh góc vuông nên \(CD \ge CH.\) Mặt khác \(CH//BA\) và \(CA \bot CH,\,\,BH \bot CH\) nên \(CHBA\) là hình chữ nhật.
Do đó \(CH = BA.\) Vì vậy \(CD \ge AB.\)
Do đó \(CA + BD\) nhỏ nhất khi và chỉ khi \(CA + BD = AB \Leftrightarrow CD = AB \Leftrightarrow CD = CH \Leftrightarrow CD//AB.\) Khi đó ta có \(ABDC\)là hình chữ nhật và do đó \(AC = BD.\) Mặt khác \(O\) là trung điểm \(AB\) nên \(M\) là trung điểm \(CD.\) Kéo theo \(CA = CM = MD = BD = R.\)
Hướng dẫn giải:
Dùng tính chất hai tiếp tuyến cắt nhau để chứng minh \(AC + BD = CD\).
Chứng minh \(CD \ge AB \Rightarrow CD\min \) khi \(CD = AB\).
