Cho tứ giác \(ABCD\) nội tiếp đường tròn tâm \(O\) bán kính bằng \(a.\) Biết rằng \(AC \bot BD.\) Khi đó để \(AB + CD\) đạt giá trị lớn nhất thì

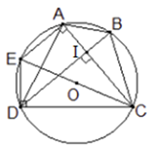
Vẽ  đường kính \(CE\) của đường tròn \(\left( O \right).\)

Ta có \(\widehat {EAC} = {90^0},\,\widehat {EDC} = {90^0}\) (góc nội tiếp chắn đường kính \(EC\) ).

Từ đó ta có \(AE \bot AC.\) Mặt khác theo giả thiết \(AC \bot BD.\)

Kéo theo \(AE//BD.\) Vậy \(AEDB\) là hình thang.

Do hình thang \(AEDB\) nội tiếp \(\left( O \right)\) nên nói phải là hình thang cân.

Kéo theo \(AB = DE\) (các cạnh bên hình thang cân).

Từ đó ta có \(A{B^2} + C{D^2} = D{E^2} + D{C^2} = E{C^2} = {\left( {2a} \right)^2} = 4{a^2}\) (do \(\Delta EDC\) vuông tại \(D).\)

Áp dụng bất đẳng thức Cô-si cho cặp số \(\left( {A{B^2},B{D^2}} \right)\) ta có $A{B^2} + B{D^2} \ge 2AB.CD \Rightarrow 2\left( {A{B^2} + B{D^2}} \right) \ge A{B^2} + B{D^2} + 2AB.CD = {\left( {AB + CD} \right)^2}.$

Kéo theo \({\left( {AB + CD} \right)^2} \le 2\left( {4{a^2}} \right) = 8{a^2} \Rightarrow AB + CD \le 2\sqrt 2 a.\)

Đẳng thức xảy ra khi và chỉ khi \(AB = CD.\)

Xét tam giác \(\Delta ABI,\,\,\Delta DCI\) có \(AB = CD,\) \(\widehat {ABD} = \widehat {ACD}\) (góc nội tiếp cùng chắn cung \(AD),\) \(\widehat {BAC} = \widehat {DCB}\) (góc nội tiếp cùng chắn cung \(BC).\)

Do đó\(\Delta ABI = \Delta DCI\left( {g.c.g} \right)\)

Kéo theo \(AI = ID,\,IB = IC.\) Suy ra \(AC = AI + IC = ID + IB = BD.\)