Cho tam giác đều \(ABC\) có cạnh bằng \(1,\) nội tiếp trong đường tròn tâm \(O.\) Đường cao \(AD\) của tam giác \(ABC\) cắt đường tròn tại điểm \(H.\) Diện tích phần giới hạn bởi cung nhỏ $BC$ và hình \(BOCH\) là:

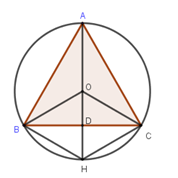
Ta có: \(AD\) là đường cao của \(\Delta ABC\) đều nên nó cũng là trung tuyến \( \Rightarrow BD = DC.\)

Xét \(\Delta DBH,\,\Delta DCH\) có

\(\begin{array}{l}BD = DC,\,\\\widehat {BDH} = \widehat {CDH} = {90^0}\\DH\,\,chung\end{array}\)\( \Rightarrow \Delta DBH = \,\Delta DCH\,\,\left( {c.g.c} \right) \Rightarrow BH = HC\,\,\left( 1 \right).\)

Do \(AH\) là đường kính nên \(\widehat {ACH} = {90^0}\). Mà $\widehat {ACD} = {60^0} \Rightarrow \widehat {DCH} = {30^0}$

Do \(OA = OC = R\) nên \(\widehat {OAC} = \widehat {OCA} = {30^0}\) suy ra \(\widehat {OCD} = {30^0}\)

Xét hai tam giác vuông \(\Delta ODC,\Delta HDC\) có \(\widehat {ODC} = \widehat {HDC} = {90^0};\widehat {OCD} = \widehat {HCD} = {30^0};CD\) chung nên \(\Delta ODC = \Delta HDC\left( {g.c.g} \right) \Rightarrow OC = CH\).

Tứ giác \(OBHC\) có 4 cạnh bằng nhau nên là hình thoi

Từ đó ta có \(OD = DH,\,BD = DC,\,\widehat {OCD} = {30^0},\,BC \bot OH\) nên:

$\begin{array}{l}{S_1} = {S_{OBHC}} = \dfrac{1}{2}BC.OH = \dfrac{1}{2}\left( {2OD} \right)\left( {2DC} \right) = 2OD.DC\\ = 2\left( {OC.\sin \,\widehat {OCD}} \right)\left( {OC.\,\cos \,\widehat {OCD}} \right)\\ = 2O{C^2}\sin \,{30^0}\,.\cos \,{30^0} = {2.1^2}.\dfrac{1}{2}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{\sqrt 3 }}{2}.\end{array}$                                      

Ta có diện tích hình quạt \(OBC\) là:

\({S_2} = \dfrac{{\pi {R^2}}}{{360}}.120 = \dfrac{\pi }{3}.\)

Vậy diện tích cần tính là \(S = {S_1} - {S_2} = \dfrac{{\sqrt 3 }}{2} - \dfrac{\pi }{3}.\)