Câu hỏi:
2 năm trước
Cho nửa đường tròn \(\left( O \right)\) đường kính \(AB\) và \(C\) là điểm chính giữa của cung \(AB.\)
Lấy điểm \(M\) thuộc cung \(BC\) và điểm \(N\) thuộc tia \(AM\) sao cho \(AN = BM.\)
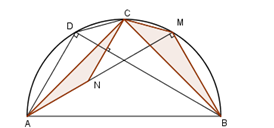
Kẻ dây \(CD\) song song với \(AM.\) Gọi \({S_1}\) \({S_2}\) lần lượt là diện tích của tam giác \(ACN\) và \(\Delta BCM.\) (hình vẽ)
Khi đó tam giác \(CMN\) là tam giác
Trả lời bởi giáo viên
Đáp án đúng: d
Theo chứng minh ở câu 14 ta có \(\Delta ACN = \Delta BCM\,.\)Do đó\(CN = CM.\)
Vì vậy \(\Delta CMN\) là tam giác cân tại \(C\,\,\left( 1 \right).\)
Lại có \(\widehat {CMA} = \dfrac{1}{2}sd\,AC = \dfrac{1}{2}{.90^0} = {45^0} \Rightarrow \widehat {CMN} = {45^0}.\)
\(\Delta CMN\) là tam giác cân tại \(C\,\)nên \(\widehat {CNM} = \widehat {CMN} = {45^0}.\) Tổng ba góc trong một tam giác bằng \({180^0}.\) Nên \(\widehat {CMN} + \widehat {CNM} + \widehat {MCN} = {180^0} \Rightarrow {45^0} + {45^0} + \widehat {MCN} = {180^0}.\)
Do đó \(\widehat {MCN} = {90^0}\,\,\left( 2 \right).\)
Từ (1) và (2) suy ra $\Delta CMN$ vuông cân tại \(C\) .
Hướng dẫn giải:
+ Chứng minh \(CN = CM.\)
+ Chứng min \(\widehat {MCN} = {90^0}\,\,.\)
