Cho hai đường tròn \(\left( {{O_1}} \right)\) và \(\left( {{O_2}} \right)\) có bán kính bằng \(R\) cắt nhau tại hai điểm \(A,\,B.\) Qua \(A\) vẽ cát tuyến cắt hai đường tròn \(\left( {{O_1}} \right)\) và \(\left( {{O_2}} \right)\) thứ tự tại \(E\) và \(F.\) \(\widehat {{O_2}A{O_1}} = {120^0}.\)  Khi đó diện tích \(S\) phần giao của hai đường tròn \(\left( {{O_1}} \right)\) và \(\left( {{O_2}} \right)\) là:

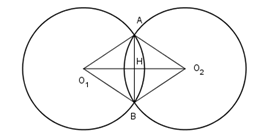
Gọi \({S_1},\,{S_2},\,{S_3}\) lần lượt là diện tích của hình quạt \(A{O_2}B,\,A{O_1}B\)

và của tứ giác \(A{O_1}B{O_2}.\) Khi đó \(S ={S_1} + {S_2} - {S_3}\) và \({S_1} = {S_2}.\)

Theo giải thiết ta có \(\widehat {{O_2}A{O_1}} = {120^0}\) nên \(\widehat {{O_2}AB} = \dfrac{1}{2}\widehat {{O_2}A{O_1}} = {60^0}.\)

Tam giác \(\Delta {O_2}AB\) cân tại \({O_2}\) nên ta nhận được \(\Delta A{O_2}B\) là tam giác đều. Từ đó \(\widehat {A{O_2}B} = {60^0}.\)

Suy ra   \({S_1} = \dfrac{{\pi {R^2}}}{{360}}.60 = \dfrac{{\pi {R^2}}}{6}.\)

Gọi \(H = {O_1}{O_2} \cap AB.\)

Xét tam giác \(AHO{_2}\) vuông tại \(H.\) Ta có \(\widehat {HA{O_2}} = {60^0},\) nên \(\sin \,{60^0} = \dfrac{{H{O_2}}}{{A{O_2}}} \Rightarrow H{O_2} = A{O_2}\sin \,{60^0} = \dfrac{{\sqrt 3 }}{2}R.\)

Áp dụng định lý Py-ta-go trong tam giác vuông \(AH{O_2}\) ta nhận được \(A{H^2} + {O_2}{H^2} = {O_2}{A^2} \Rightarrow A{H^2} = {O_2}{A^2} - {O_2}{H^2} = \dfrac{{{R^2}}}{4} \Rightarrow AH = \dfrac{R}{2}.\)

Diện tích tam giác \(AH{O_2}\) là \(\dfrac{1}{2}AH.H{O_2} = \dfrac{1}{2}.\left( {\dfrac{R}{2}} \right)\left( {\dfrac{{\sqrt 3 R}}{2}} \right) = \dfrac{{\sqrt 3 {R^2}}}{8}.\) Ta có thể kiểm tra được các tam giác \(\Delta AH{O_2},\,\Delta BH{O_2},\,\Delta AH{O_1},\,\Delta BH{O_1}\) là các tam giác bằng nhau. Do đó diện tích của tứ giác \(A{O_2}B{O_1}\) bằng \(4\) lần diện tích tam giác \(AH{O_2}.\) Do đó \({S_3} = 4.\left( {\dfrac{{\sqrt 3 {R^2}}}{8}} \right) = \dfrac{{\sqrt 3 }}{2}{R^2}.\)

Từ đó ta có:

\(\begin{array}{l}S = {S_1} + {S_2} - {S_3}\\ = \dfrac{{\pi {R^2}}}{6} + \dfrac{{\pi {R^2}}}{6} - \dfrac{{\sqrt 3 {R^2}}}{2}\\ = \dfrac{{{R^2}\left( {2\pi  - 3\sqrt 3 } \right)}}{6}\end{array}\)