Câu hỏi:
2 năm trước
Cho nửa đường tròn \(\left( O \right)\) đường kính \(AB\) và \(C\) là điểm chính giữa của cung \(AB.\)
Lấy điểm \(M\) thuộc cung \(BC\) và điểm \(N\) thuộc tia \(AM\) sao cho \(AN = BM.\)
Kẻ dây \(CD\) song song với \(AM.\) Gọi \({S_1}\) \({S_2}\) lần lượt là diện tích của tam giác \(ACN\) và \(\Delta BCM.\) (hình vẽ)
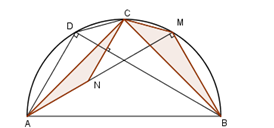
Chọn câu đúng.
Trả lời bởi giáo viên
Đáp án đúng: c
Xét \(\Delta ACN\) và \(\Delta BCM\) có:
+ \(AC = BC\) (vì \(C\) là điểm chính giữa của cung \(AB\))
+ \(\widehat {CAN} = \widehat {CBN}\) (hai góc nội tiếp cùng chắn cung \(CM\))
+ Theo giả thiết ta có \(AN = BM.\)
Do đó \(\Delta ACN = \Delta BCM\,\,\left( {c.g.c} \right).\) Hai tam giác bằng nhau nên diện tích bằng nhau. Do đó \({S_1} = {S_2}.\)
Hướng dẫn giải:
Chứng minh hai tam giác bằng nhau \(\Delta ACN\) và \(\Delta BCM\) từ đó suy ra mối quan hệ về diện tích.
