Câu hỏi:
2 năm trước
Cho đường tròn \(\left( {O;R} \right)\) và một điểm \(M\) nằm ở ngoài đường tròn sao cho \(MO = 2R.\) Đường thẳng \(d\) đi qua \(M,\) tiếp xúc với đường tròn \(\left( {O;R} \right)\) tại \(A.\) Giả sử \(N = MO \cap \left( {O;R} \right).\) Kẻ hai đường kính \(AB,\,\,CD\) khác nhau của \(\left( {O;R.} \right)\) Các đường thẳng \(BC,\,BD\) cắt đường thẳng \(d\) lần lượt tại \(P,Q.\) Khi đó
Trả lời bởi giáo viên
Đáp án đúng: a
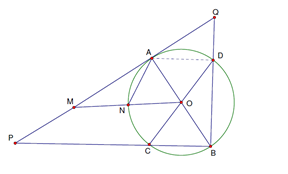
Xét \(\Delta QAB\) vuông ở \(A\) ta có \(AD \bot QB.\) Suy ra \(QB.DB = A{B^2} = 4{R^2}\) và \(QB.QD = A{Q^2}.\)
Ta có:
\(\begin{array}{l}QB > BD \Rightarrow {\left( {\sqrt {QB} - \sqrt {BD} } \right)^2} > 0\\ \Rightarrow BQ + BD > 2\sqrt {BQ.BD} = 4R\,\left( 3 \right).\end{array}\)
Tương tự ta có \(QB + QD > 2\sqrt {QB.QD} = 2AQ\,\,\left( 4 \right),\)
Cộng từng vế của \(\left( 3 \right)\) và \(\left( 4 \right)\) ta nhận được \(2QB + DB + QD > 4R + 2AQ \Rightarrow 3QB - 2AQ > 4R.\)
Hướng dẫn giải:
- Sử dụng các hệ thức giữa ạnh và dường cao trong tam giác vuông, kết hợp với bất đẳng thức Cô-si để đánh giá các tổng \(BQ + BD\) và \(BQ + DQ\).
