Câu hỏi:
3 năm trước
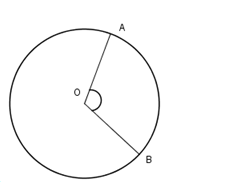
Cho biết diện tích của hình quạt \(OAB\) bằng \(\dfrac{1}{4}\) diện tích của hình tròn. Khi đó \(\widehat {BOA} = ?\)
Trả lời bởi giáo viên
Đáp án đúng: a
Đặt \(\alpha = \widehat {BOA}.\) Giả sử rằng \(R\) là bán kính của hình tròn. Khi đó ta có \({S_{OAB}} = \dfrac{{\pi {R^2}}}{{360}}.\alpha .\)
Mặt khác diện tích của hình tròn là \(S = \pi {R^2}.\)
Theo giả thiết ta có \({S_{OAB}} = \dfrac{1}{4}S \Rightarrow \dfrac{{\pi {R^2}}}{{360}}\alpha = \dfrac{1}{4}\left( {\pi {R^2}} \right) \Rightarrow \alpha = {90^0}.\)
Hướng dẫn giải:
Dựa và công thức tính diện tích hình quạt tròn có góc ở tâm \(\alpha \) là \({S_{OAB}} = \dfrac{{\pi {R^2}}}{{360}}.\alpha .\)
Dựa và mối quan hệ diện tích của hình quạt tròn và hình tròn để tìm \(\alpha \).

