Ôn tập chương 4 - Dao động và sóng điện từ

Ta có: $\left\{ \begin{array}{l}q = {Q_0}\cos \left( {\omega t + \varphi } \right)\\i = q' =  - \omega {Q_0}\sin \left( {\omega t + \varphi } \right) = {I_0}\cos \left( {\omega t + \varphi  + \dfrac{\pi }{2}} \right)\end{array} \right.$

 => $i$ sớm pha $\dfrac{\pi }{2}$ so với $q$

Ta có:   ${\left( {\dfrac{i}{{{I_0}}}} \right)^2} + {\left( {\dfrac{q}{{{Q_0}}}} \right)^2} = 1$

Tại :  \(t = \frac{{\pi {\rm{}}}}{{20}}\mu s\)  thay vào phương trình $i$ , ta có:

$i{\rm{ }} = 2\cos \left( {{{2.10}^7}.\dfrac{\pi }{{20}}{{.10}^{ - 6}} + \dfrac{\pi }{2}} \right) = 0\left( A \right)$

$ \to q = {Q_0} = \dfrac{{{I_0}}}{\omega } = \dfrac{{{{2.10}^{ - 3}}}}{{{{2.10}^7}}} = {10^{ - 10}}C = 0,1nC$

Ta có: $\left\{ \begin{array}{l}{f_1} = \dfrac{1}{{2\pi \sqrt {L{C_1}} }}\\{f_2} = \dfrac{1}{{2\pi \sqrt {L{C_2}} }} = \dfrac{1}{{2\pi \sqrt {L.4{C_1}} }} = \dfrac{{{f_1}}}{2} = 0,5{f_1}\end{array} \right.$

Gọi độ lệch pha giữa ${q_1}$ và ${q_2}$ là $\Delta \varphi $

Tại thời điểm ${q_1} = 0$ thì  ${i_1} = {I_{o1}} = {Q_1}\omega $ và  ${q_2} = {Q_2}cos\Delta \varphi $ thay vào phương trình ${q_1}{i_2} + {q_2}{i_1} = {6.10^{ - 9}}$  ta được:

\({Q_1}{Q_2}\omega cos\Delta \varphi {\rm{}} = {6.10^{ - 9}} \to \omega {\rm{}} = \frac{{{{6.10}^{ - 9}}}}{{{Q_1}{Q_2}cos\Delta \varphi }}\)

Ta có:

$\begin{array}{l}{Q_1} + {Q_2} \ge 2\sqrt {{Q_1}{Q_2}} \\ \to {Q_1}{Q_2} \le \dfrac{{{{\left( {{Q_1} + {Q_2}} \right)}^2}}}{4} = \dfrac{{{{\left( {{{8.10}^{ - 6}}} \right)}^2}}}{4} = 1,{6.10^{ - 11}}\end{array}$

Và  \(\left| {cos\Delta \varphi } \right|{\rm{}} \le 1\)

Kết hợp (1) ta suy ra: \(\omega  \ge \dfrac{{{{6.10}^{ - 9}}}}{{1,{{6.10}^{ - 11}}}} = 375rad/s\)

Lại có: \(f = \dfrac{\omega }{{2\pi }} \to f \ge \dfrac{{375}}{{2\pi }} = 59,683Hz\)

Nếu mạch dao động luôn có \({U_0} = {\rm{ }}12V\) thì về mặt năng lượng ta có:

\({W_{tmax}} = {\rm{ }}{W_{dmax}}\)

  $\begin{array}{l} \Leftrightarrow \dfrac{1}{2}L.I_0^2 = \dfrac{1}{2}C.U_0^2\\ \Rightarrow {I_0} = \sqrt {\dfrac{{C.U_0^2}}{L}}  = \sqrt {\dfrac{{{{5.10}^{ - 6}}{{.12}^2}}}{{{{50.10}^{ - 3}}}}}  = {12.10^{ - 2}}A\\ \Rightarrow P = R.{I^2} = R.{\left( {\dfrac{{{I_0}}}{{\sqrt 2 }}} \right)^2} = {72.10^{ - 6}}{\rm{W}}\end{array}$

=> Công suất cần cung cấp cho mạch là: \(P = 72\mu {\rm{W}}\)

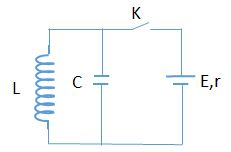
+ Ta có: \(T = 2\pi \sqrt {LC} {\rm{}}\)

=> Độ tự cảm của cuộn dây:  $L = \dfrac{{{T^2}}}{{4{\pi ^2}C}} = \dfrac{{{{\left( {\pi {{.10}^{ - 6}}} \right)}^2}}}{{4{\pi ^2}.2,{{5.10}^{ - 7}}}} = {10^{ - 6}}H$

+ Cường độ dòng điện cực đại chạy qua cuộn dây:  ${I_0} = \dfrac{E}{r}$

+ Hiệu điện thế cực đại trên tụ:  \({U_{0}} = {\rm{ }}2E\)

\(\dfrac{{LI_0^2}}{2} = \dfrac{{CU_0^2}}{2} \Leftrightarrow L\dfrac{{{E^2}}}{{{r^2}}} = C.4.{E^2} \Rightarrow r = \sqrt {\dfrac{L}{{4C}}} {\rm{}} = \sqrt {\dfrac{{{{10}^{ - 6}}}}{{{{4.2,5.10}^{ - 7}}}}} {\rm{}} = 1\Omega \)

Điện tích cực đại của tụ là :  ${Q_0} = \dfrac{{{I_0}}}{\omega } = \dfrac{{0,04}}{{{{2.10}^7}}} = {2.10^{ - 9}}C$

Tần số góc của mạch 1 và mạch 2:  ${\omega _1} = {\omega _2} = \dfrac{1}{{\sqrt {{L_1}{C_1}} }} = \dfrac{1}{{\sqrt {{{2.10}^{ - 6}}.0,{{2.10}^{ - 6}}} }} = 5\pi {.10^5}(rad/s)$

Phương trình hiệu điện thế của mạch 1 và mạch 2:  $\left\{ \begin{array}{l}{u_1} = 8\cos \left( {5\pi {{.10}^5}t} \right)\\{u_2} = 16\cos \left( {5\pi {{.10}^5}t} \right)\end{array} \right. \Rightarrow \Delta u = {u_2} - {u_1} = 8\cos \left( {5\pi {{.10}^5}t} \right)$

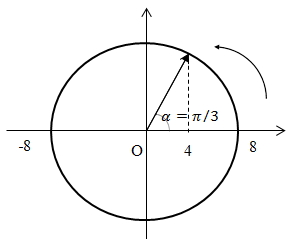
Biểu diễn trên đường tròn lượng giác ta có: 

Góc quét được :  \(\alpha {\rm{}} = \dfrac{{\pi {\rm{}}}}{3} \Rightarrow \Delta t = \dfrac{{\alpha {\rm{}}}}{\omega } = \dfrac{{\pi {\rm{}}}}{{3.5\pi {{.10}^5}}} = \dfrac{{{{2.10}^{ - 6}}}}{3}s\)

Áp dụng công thức tính năng lượng mạch dao động ta có:

\(\dfrac{1}{2}C{u^2} + \dfrac{1}{2}L{i^2} = \dfrac{1}{2}CU_0^2\)

\( \Leftrightarrow \dfrac{1}{2}{.8.10^{ - 9}}.{u^2} + \dfrac{1}{2}{.2.10^{ - 3}}.{({6.10^{ - 3}})^2} = \dfrac{1}{2}{.8.10^{ - 9}}{.6^2}\)

\( =  > u = 3\sqrt 3 V\)

Bước sóng điện từ được xác định theo công thức: \(\lambda {\rm{}} = cT = c2\pi \sqrt {LC} \)

Ta có tỉ số: $\dfrac{{{C_2}}}{{{C_1}}} = \dfrac{{\lambda _2^2}}{{\lambda _1^2}} = \dfrac{{{{1000}^2}}}{{{{100}^2}}} = 100$

+ Do cảm ứng từ và cường độ điện trường biến thiên cùng pha, ta suy ra phương trình của cường độ điện trường: $E = {E_0}cos\left( {2\pi {{.10}^6}t} \right)$

+ Chu kì: $T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{2\pi {{.10}^6}}} = {10^{ - 6}}s = 1\mu s$

+ Tại thời điểm \(t = 0\) cường độ điện trường \(E = {E_0}cos0 = {E_0}\)

Biểu diễn trên đường tròn lượng giác:

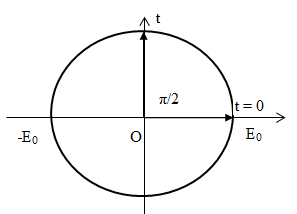
Kể từ lúc $t{\rm{ }} = {\rm{ }}0$, thời điểm đầu tiên cường độ điện trường bằng $0$ là: $t = \dfrac{T}{4} = \dfrac{10^{-6}}{4} = 0,25\mu s$

Ta có: \(\frac{{{i^2}}}{{I_0^2}} + \frac{{{u^2}}}{{U_0^2}} = 1 \Rightarrow i = {I_0}\sqrt {1 - \frac{{{u^2}}}{{U_0^2}}} {\rm{}} = {U_0}\sqrt {\frac{C}{L}} .\sqrt {1 - {{0,8}^2}} {\rm{}} = \frac{{3{U_0}}}{5}\sqrt {\frac{C}{L}} \)

Vì $u{\rm{ }} = {\rm{ }}0,8{U_0}$ và tụ đang tích điện, nghĩa là đang tăng mà $i$ nhanh pha hơn $u$ góc \(\dfrac{\pi }{2}\) nên khi đó $i$ đang giảm

Ta có: $\dfrac{{\Delta {\rm{W}}}}{{\rm{W}}} = \dfrac{{I_0^2 - {I'^2}}}{{I_0^2}} = \dfrac{{\left( {{I_0} - I'} \right)\left( {{I_0} + I'} \right)}}{{I_0^2}} = \dfrac{{\Delta I}}{{{I_0}}}\dfrac{{\left( {2{I_0} - \Delta I} \right)}}{{{I_0}}} = \dfrac{{\Delta I}}{{{I_0}}}\left( {2 - \dfrac{{\Delta I}}{{{I_0}}}} \right) = 0,19$

Với $x = \dfrac{{\Delta I}}{{{I_0}}}$ ta có  ${x^2} - 2x + 0,19 = 0 \to x = 0,1$

=> Biên độ dòng điện giảm \(10\% \)

Ta có:

\(\begin{array}{l}\dfrac{1}{2}.C.{u^2} + \dfrac{1}{2}L.{i^2} = \dfrac{1}{2}.L.I_0^2\\ \Rightarrow (n + 1).L.{i^2} = L.I_0^2\\ \Rightarrow i =  \pm \dfrac{{{I_0}}}{{\sqrt {n + 1} }}\end{array}\)

+ Công thức tính tần số mạch dao động là:$f = \dfrac{1}{{2\pi \sqrt {LC} }}$

+ Công thức tính điện dung của tụ mắc nối tiếp là: $\dfrac{1}{C} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}$

$\begin{array}{l} \to {f^2} = f_1^2 + f_2^2 = {75^2} + {(50\sqrt {10} )^2}\\ \to f = 175MHz\end{array}$

+ Ta có công thức tính chu kì của mạch dao động là: $T = 2\pi \sqrt {LC} $

+ Khi tụ mắc song song với nhau thì công thức tính điện dung tương đương là: $C = {C_1} + {C_2}$

Suy ra công thức tính chu kì của mạch có tụ mắc song song là: ${T^2} = T_1^2 + T_2^2{\rm{ }} =  > T = \sqrt {T_1^2 + T_2^2}  = 1,{3.10^{ - 4}}s{\rm{ }}$

Cứ sau mỗi nửa chu kì thì $q$ lại có độ lớn cực đại.

Ta có:
 $\begin{array}{*{20}{l}}{T = \dfrac{{2\pi }}{\omega } = 2\pi \sqrt {LC}  = 2\pi \sqrt {{{5.10}^{ - 3}}{{.5.10}^{ - 9}}}  = \pi {{.10}^{ - 5}}s}\\{ =  > \Delta t = \dfrac{T}{2} = 5\pi {{.10}^{ - 6}}s}\end{array}$

Ta có cường độ dòng điện cực đại trong mạch: \({I_0} = \omega {Q_0}\)

Lại có \(T = \dfrac{{2\pi }}{\omega }\)

=> Chu kỳ dao động điện từ của mạch là:  $T = \dfrac{{2\pi }}{\omega } = 2\pi \dfrac{{{Q_0}}}{{{I_0}}}$

+ Ta có phương trình điện tích :  $q = {Q_0}.\cos \left( {\omega t + \varphi } \right)$

+ Ban đầu bản $A$ tích điện \(\dfrac{{{Q_0}}}{2}\) và đang tăng nên pha ban đầu có giá trị $\varphi  = \dfrac{{ - \pi }}{3}$

+ Khi bản $B$ có điện tích cực đại ${Q_0}$ thì bản $A$ có điện tích $-{Q_0}$ .

Ta có vecto quay như hình vẽ:

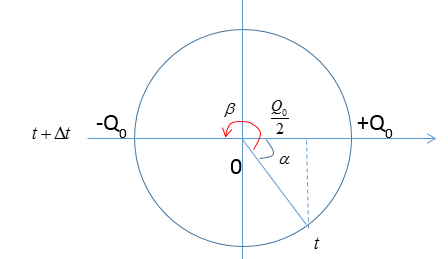
Ta có:

\(\begin{array}{l}cos\alpha  = \dfrac{{\dfrac{{{Q_0}}}{2}}}{{{Q_0}}} = \dfrac{1}{2} \to \alpha  = \dfrac{\pi }{3}\\ \to \beta  = \pi  + \dfrac{\pi }{3} = \dfrac{{4\pi }}{3}\end{array}\)

Mặt khác, ta có:

\(\begin{array}{l}\beta  = \omega \Delta t = \dfrac{{2\pi }}{T}\Delta t\\ \to \Delta t = \dfrac{\beta }{{2\pi }}T = \dfrac{{\dfrac{{4\pi }}{3}}}{{2\pi }}T = \dfrac{2}{3}T\end{array}\)

+ Giả sử phương trình điện tích là : $q = {Q_0}.\cos \left( {\omega t + \varphi } \right)$

+ Phương trình cường độ dòng điện là :  $i = q' =  - \omega .{Q_0}.\sin \left( {\omega t + \varphi } \right) = {I_0}.\cos \left( {\omega t + \varphi  + \dfrac{\pi }{2}} \right)$

Tụ đang phóng điện tức là $q$ đang giảm

Vì q đang giảm nên I đang tăng => Lấy vị trí thứ (2)

=> Ta có phương trình của i là :  $i = {I_0}.\cos \left( {\omega t - \dfrac{\pi }{3}} \right)$

Với tần số góc: $\omega  = \dfrac{1}{{\sqrt {LC} }} = {5.10^5}rad/s$

Khi năng lượng điện trường bằng một nửa năng lượng từ trường cực đại thì năng lượng từ trường cũng bằng một nửa năng lượng từ trường cực đại nên :

\(\begin{array}{*{20}{l}}{\dfrac{1}{2}L{i^2} = \dfrac{1}{2}.\dfrac{1}{2}LI_0^2}\\\begin{array}{l} \to I_0^2 = 2{i^2} = 2{\left( {\sqrt 2 } \right)^2} = 4\\ \to {I_0} = 2A\end{array}\end{array}\)

Vậy phương trình của dòng điện I là: $i = 2.\cos \left( {{{5.10}^5}t - \dfrac{\pi }{3}} \right)A$