Một tụ xoay có điện dung biến thiên theo hàm số bậc nhất với góc quay từ giá trị \({C_{1}} = {\rm{ }}10pF\) đến \({C_{2}} = {\rm{ }}370pF\) tương ứng góc quay của các bản tăng dần từ \({0^0}\) đến ${180^0}$. Tụ điện được mắc với một cuộn dây thuần cảm có \(L = 2\mu H\) để tạo thành mạch chọn sóng của máy thu. Để thu được bước sóng 22,3m thì phải xoay tụ một góc bằng bao nhiêu kể từ vị trí điện dung cực đại.
+ Điện dung của tụ phụ thuộc góc quay của bản tụ: \(C = a\alpha + b\)
+ Với hai giá trị lớn nhất và nhỏ nhất của điện dụng là ${C_1}$ và ${C_2}$, ta có:
\(\left\{ {\begin{array}{*{20}{l}}{a.0 + b = 10(pF)}\\{a.180 + b = 370(pF)}\end{array}} \right. \to \left\{ {\begin{array}{*{20}{l}}{a = 2(pF)}\\{b = 10(pF)}\end{array}} \right. \to C = 2.\alpha {\rm{}} + 10(pF)(1)\)
+ Để bắt được sóng có bước sóng $\lambda {\rm{ }} = {\rm{ }}22,3{\rm{ }}m$ thì điện dung của tụ bằng $C = \dfrac{{{\lambda ^2}}}{{4{\pi ^2}{c^2}L}} = {70.10^{ - 12}}(F) = 70(pF)$
Thay vào (1) tìm được $\alpha {\rm{ }} = {\rm{ }}{30^0}$
Vậy phải tụ phải quay một góc bằng ${150^0}$ từ vị trí có điện dung cực đại (ứng với góc ${180^0}$)
Trong mạch dao động $LC$ lí tưởng với cường độ dòng điện cực đại là ${I_0}$ và dòng điện biến thiên với tần số góc bằng \(\omega \). Trong khoảng thời gian cường độ dòng điện giảm từ giá trị cực đại đến một nửa cực đại thì điện lượng chuyển qua cuộn dây có độ lớn bằng:
+ Cường độ dòng điện trong mạch $LC$ sớm pha $\dfrac{\pi }{2}$ so với điện lượng.
+ Nên khi ban đầu cường độ dòng điện cực đại thì điện lượng bằng $0$, cường độ dòng điện đang giảm thì $q$ đang tăng.
$\begin{array}{l}i = \dfrac{{{I_0}}}{2} \Rightarrow {\varphi _i} = \dfrac{\pi }{3} \Rightarrow {\varphi _q} = \dfrac{\pi }{3} - \dfrac{\pi }{2} = \dfrac{{ - \pi }}{6}\\ \Rightarrow q = \dfrac{{{I_0}}}{\omega }.\cos \left( {\dfrac{{ - \pi }}{6}} \right) = \dfrac{{\sqrt 3 }}{2}\dfrac{{{I_0}}}{\omega }\\ \Rightarrow \Delta q = q - 0 = \dfrac{{\sqrt 3 }}{2}\dfrac{{{I_0}}}{\omega }\end{array}$
Một sóng điện từ truyền trong chân không với bước sóng $150{\rm{ }}m$, cường độ điện trường cực đại và cảm ứng từ cực đại của sóng lần lượt là ${E_0}$ và ${B_0}$.Tại thời điểm nào đó, cường độ điện trường tại một điểm trên phương truyền sóng có giá trị $\dfrac{{{E_0}\sqrt 3 }}{2}$ và đang tăng. Sau thời gian ngắn nhất là bao nhiêu thì cảm ứng từ tại điểm đó có giá trị bằng $\dfrac{{{B_0}}}{2}$?
Theo bài ra ta có tại thời điểm t: $E = \dfrac{{{E_0}\sqrt 3 }}{3} = > B = \dfrac{{{B_0}\sqrt 3 }}{3}$ ( đang tăng)
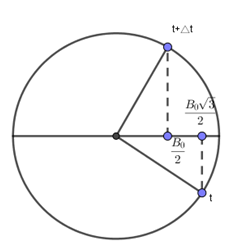
$T = \dfrac{\lambda }{c} = \dfrac{{150}}{{{{3.10}^8}}} = {5.10^{ - 7}}s$
Thời gian ngắn nhất cảm ứng từ tại điểm đó có giá trị bằng $\dfrac{{{B_0}}}{2}$là:
\(\Delta t = \dfrac{T}{{12}} + \dfrac{T}{6} = \dfrac{T}{4} = \dfrac{{{{5.10}^{ - 7}}}}{4} = 1,{25.10^{ - 7}}s = 125ns\)
Trong nguyên tắc thông tin liên lạc bằng sóng vô tuyến, biến điệu sóng là:
Trong truyền thông bằng sóng điện từ thì biến điệu sóng là trộn sóng âm tần với sóng cao tần.
Trong một mạch dao động $LC$ lí tưởng, cường độ dòng điện trong mạch có biểu thức $i = 0,4\cos \left( {{{2.10}^6}t - \dfrac{\pi }{2}} \right)A$. Điện tích trên tụ có biểu thức là:
Ta có:
$\begin{array}{l}i = q' \to q = \int\limits_0^t {idt = \int\limits_0^t {0,4\cos \left( {{{2.10}^6}t - \dfrac{\pi }{2}} \right)dt} } \\ = \dfrac{{0,4}}{{{{2.10}^{ - 6}}}}.\sin \left( {{{2.10}^6}t - \dfrac{\pi }{2}} \right)\left| \begin{array}{l}t\\0\end{array} \right.\\ = 0,2\cos \left( {{{2.10}^{ - 6}}t - \pi } \right)\mu C\end{array}$
Một vật phát sóng điện từ dùng mạch \(LC\) lý tưởng. Biết điện tích cực đại trên một bản tụ là 2nC và dòng điện cực đại qua cuộn cảm là \(0,3A\). Sóng điện từ do mạch dao độn này phát ra thuộc loại:
Ta có,
\(I_0=\omega Q_0\)
=> \(\omega = \dfrac{I_0}{Q_0}\)
Lại có: \(\omega=2\pi f=> f=\dfrac{\omega}{2\pi}=\dfrac{I_0}{2\pi Q_0}\)
+ Bước sóng mà mạch dao động phát ra là \(\lambda = \dfrac{c}{f} = 2\pi c \dfrac{{{Q_0}}}{{{I_0}}} = 2\pi {3.10^8}\dfrac{{{{2.10}^{ - 9}}}}{{0,3}} = 12,56m\) thuộc vùng sóng ngắn
