Một sóng điện từ truyền trong chân không với bước sóng $150{\rm{ }}m$, cường độ điện trường cực đại và cảm ứng từ cực đại của sóng lần lượt là ${E_0}$ và ${B_0}$.Tại thời điểm nào đó, cường độ điện trường tại một điểm trên phương truyền sóng có giá trị $\dfrac{{{E_0}\sqrt 3 }}{2}$ và đang tăng. Sau thời gian ngắn nhất là bao nhiêu thì cảm ứng từ tại điểm đó có giá trị bằng $\dfrac{{{B_0}}}{2}$?
Trả lời bởi giáo viên
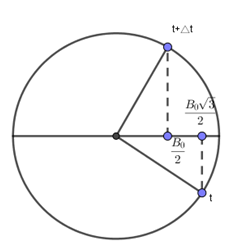
Theo bài ra ta có tại thời điểm t: $E = \dfrac{{{E_0}\sqrt 3 }}{3} = > B = \dfrac{{{B_0}\sqrt 3 }}{3}$ ( đang tăng)
$T = \dfrac{\lambda }{c} = \dfrac{{150}}{{{{3.10}^8}}} = {5.10^{ - 7}}s$
Thời gian ngắn nhất cảm ứng từ tại điểm đó có giá trị bằng $\dfrac{{{B_0}}}{2}$là:
\(\Delta t = \dfrac{T}{{12}} + \dfrac{T}{6} = \dfrac{T}{4} = \dfrac{{{{5.10}^{ - 7}}}}{4} = 1,{25.10^{ - 7}}s = 125ns\)
Hướng dẫn giải:
+ Áp dụng vòng tròn lượng giác trong dao đông điện từ
+ Vận dụng biểu thức tính bước sóng: \(\lambda = cT\)

