Tại một điểm có sóng điện từ truyền qua, cảm ứng từ biến thiên theo phương trình $B = {B_0}\cos (2\pi {.10^6}t)$ (t tính bằng s). Kể từ lúc $t{\rm{ }} = {\rm{ }}0$, thời điểm đầu tiên để cường độ điện trường tại điểm đó bằng $0$ là:
Trả lời bởi giáo viên
+ Do cảm ứng từ và cường độ điện trường biến thiên cùng pha, ta suy ra phương trình của cường độ điện trường: $E = {E_0}cos\left( {2\pi {{.10}^6}t} \right)$
+ Chu kì: $T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{2\pi {{.10}^6}}} = {10^{ - 6}}s = 1\mu s$
+ Tại thời điểm \(t = 0\) cường độ điện trường \(E = {E_0}cos0 = {E_0}\)
Biểu diễn trên đường tròn lượng giác:
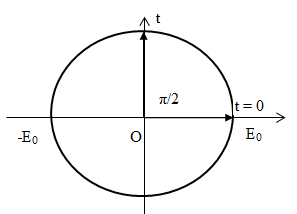
Kể từ lúc $t{\rm{ }} = {\rm{ }}0$, thời điểm đầu tiên cường độ điện trường bằng $0$ là: $t = \dfrac{T}{4} = \dfrac{10^{-6}}{4} = 0,25\mu s$
Hướng dẫn giải:
+ Sử dụng lí thuyết về pha dao động của cảm ứng từ và điện trường: Tại một thời điểm có sóng điện từ truyền qua, cảm ứng từ và cường độ điện trường biến thiên cùng pha
+ Sử dụng biểu thức tính chu kì: \(T = \dfrac{{2\pi }}{\omega }\)
+ Sử dụng vòng tròn lượng giác

