Một mạch dao động $LC$ lí tưởng gồm cuộn cảm thuần $L$ và tụ điện $C$ có hai bản $A$ và $B$. Trong mạch đang có dao động điện từ tự do với chu kì $T$, biên độ điện tích của tụ điện bằng ${Q_0}$. Tại thời điểm $t$, điện tích bản $A$ là ${q_A} = \dfrac{{{Q_0}}}{2}$ và đang tăng. Sau khoảng thời gian $\Delta t$ nhỏ nhất thì điện tích của bản $B$ là ${q_B} = {\rm{ }}{Q_0}$. Giá trị của $\Delta t$ là:
Trả lời bởi giáo viên
+ Ta có phương trình điện tích : $q = {Q_0}.\cos \left( {\omega t + \varphi } \right)$
+ Ban đầu bản $A$ tích điện \(\dfrac{{{Q_0}}}{2}\) và đang tăng nên pha ban đầu có giá trị $\varphi = \dfrac{{ - \pi }}{3}$
+ Khi bản $B$ có điện tích cực đại ${Q_0}$ thì bản $A$ có điện tích $-{Q_0}$ .
Ta có vecto quay như hình vẽ:
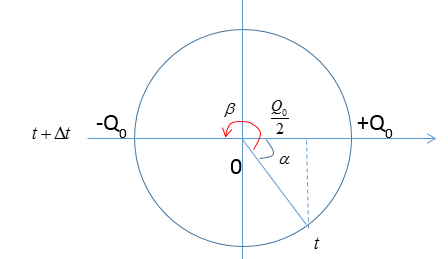
Ta có:
\(\begin{array}{l}cos\alpha = \dfrac{{\dfrac{{{Q_0}}}{2}}}{{{Q_0}}} = \dfrac{1}{2} \to \alpha = \dfrac{\pi }{3}\\ \to \beta = \pi + \dfrac{\pi }{3} = \dfrac{{4\pi }}{3}\end{array}\)
Mặt khác, ta có:
\(\begin{array}{l}\beta = \omega \Delta t = \dfrac{{2\pi }}{T}\Delta t\\ \to \Delta t = \dfrac{\beta }{{2\pi }}T = \dfrac{{\dfrac{{4\pi }}{3}}}{{2\pi }}T = \dfrac{2}{3}T\end{array}\)
Hướng dẫn giải:
+ Sử dụng công thức tính thời gian bằng đường tròn.
+ Sử dụng biểu thức: \(\Delta \varphi = \omega \Delta t\)

