Câu hỏi:
2 năm trước
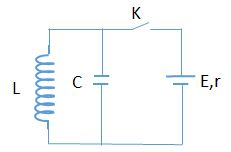
Cho mạch điện như hình vẽ bên, nguồn điện một chiều có suất điện động $E$ không đổi và điện trở trong $r$, cuộn dây thuần cảm $L$ và tụ điện có điện dung \(C{\rm{ }} = {\rm{ }}2,{5.10^{ - 7}}F\). Ban đầu khoá $K$ mở, tụ chưa tích điện. Đóng khoá $K$, khi mạch ổn định thì mở khoá $K$. Lúc này trong mạch có dao động điện từ tự do với chu kì bằng $\pi {.10^{ - 6}}s$ và hiệu điện thế cực đại trên tụ bằng $2E$. Giá trị của $r$ gần với giá trị nào nhất sau đây?
Trả lời bởi giáo viên
Đáp án đúng: c
+ Ta có: \(T = 2\pi \sqrt {LC} {\rm{}}\)
=> Độ tự cảm của cuộn dây: $L = \dfrac{{{T^2}}}{{4{\pi ^2}C}} = \dfrac{{{{\left( {\pi {{.10}^{ - 6}}} \right)}^2}}}{{4{\pi ^2}.2,{{5.10}^{ - 7}}}} = {10^{ - 6}}H$
+ Cường độ dòng điện cực đại chạy qua cuộn dây: ${I_0} = \dfrac{E}{r}$
+ Hiệu điện thế cực đại trên tụ: \({U_{0}} = {\rm{ }}2E\)
\(\dfrac{{LI_0^2}}{2} = \dfrac{{CU_0^2}}{2} \Leftrightarrow L\dfrac{{{E^2}}}{{{r^2}}} = C.4.{E^2} \Rightarrow r = \sqrt {\dfrac{L}{{4C}}} {\rm{}} = \sqrt {\dfrac{{{{10}^{ - 6}}}}{{{{4.2,5.10}^{ - 7}}}}} {\rm{}} = 1\Omega \)
Hướng dẫn giải:
+ Sử dụng biểu thức tính chu kì: \(T = 2\pi \sqrt {LC} \)
+ Sử dụng biểu thức định luật Ôm: $I = \dfrac{E}{r}$
+ Sử dụng định luật bảo toàn năng lượng điện từ ${{\rm{W}}_{LC}} = \dfrac{{LI_0^2}}{2} = \dfrac{{CU_0^2}}{2}$
Câu hỏi khác
- Bài tập mạch dao động LC các đại lượng đặc trưng có lời giải MÔN LÝ lớp 12
- Bài tập năng lượng của mạch dao động LC có lời giải MÔN LÝ lớp 12
- Bài tập phương trình dao động mạch LC q,u,i có lời giải MÔN LÝ lớp 12
- Bài tập điện từ trường - sóng điện từ lý 12 có lời giải
- Bài tập các loại dao động lý 12 có lời giải
