Có hai tụ điện ${C_1},{\rm{ }}{C_2}$ và hai cuộn cảm thuần ${L_1},{\rm{ }}{L_2}$. Biết \({C_1} = {\rm{ }}{C_2} = {\rm{ }}0,2\mu F\), ${L_1} = {L_2} = 2\mu H$. Ban đầu tích điện cho tụ ${C_1}$ đến hiệu điện thế $8V$ và tụ ${C_2}$ đến hiệu điện thế $16V$ rồi cùng một lúc mắc ${C_1}$ với ${L_1},{\rm{ }}{C_2}$ với ${L_2}$ để tạo thành mạch dao động lí tưởng ${L_1}{C_1}$ và ${L_2}{C_2}$. Lấy \({\pi ^{2}} = {\rm{ }}10\). Thời gian ngắn nhất kể từ khi hai mạch bắt đầu dao động đến khi hiệu điện thế trên hai tụ ${C_1}$ và ${C_2}$ chênh lệch nhau $4V$ là:
Trả lời bởi giáo viên
Tần số góc của mạch 1 và mạch 2: ${\omega _1} = {\omega _2} = \dfrac{1}{{\sqrt {{L_1}{C_1}} }} = \dfrac{1}{{\sqrt {{{2.10}^{ - 6}}.0,{{2.10}^{ - 6}}} }} = 5\pi {.10^5}(rad/s)$
Phương trình hiệu điện thế của mạch 1 và mạch 2: $\left\{ \begin{array}{l}{u_1} = 8\cos \left( {5\pi {{.10}^5}t} \right)\\{u_2} = 16\cos \left( {5\pi {{.10}^5}t} \right)\end{array} \right. \Rightarrow \Delta u = {u_2} - {u_1} = 8\cos \left( {5\pi {{.10}^5}t} \right)$
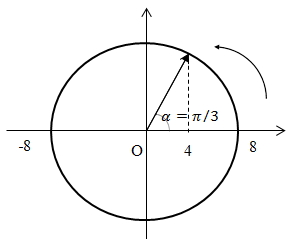
Biểu diễn trên đường tròn lượng giác ta có:
Góc quét được : \(\alpha {\rm{}} = \dfrac{{\pi {\rm{}}}}{3} \Rightarrow \Delta t = \dfrac{{\alpha {\rm{}}}}{\omega } = \dfrac{{\pi {\rm{}}}}{{3.5\pi {{.10}^5}}} = \dfrac{{{{2.10}^{ - 6}}}}{3}s\)
Hướng dẫn giải:
+ Sử dụng biểu thức tính tần số góc của mạch dao động LC: \(\omega = \dfrac{1}{{\sqrt {LC} }}\)
+ Sử dụng đường tròn lượng giác
+ Vận dụng biểu thức: \(\Delta \varphi = \omega \Delta t\)

