Một con lắc lò xo dao động điều hòa. Lực kéo về tác dụng lên vật luôn:
Lực kéo về tác dụng lên vật luôn hướng về vị trí cân bằng.
Một con lắc lò xo có độ cứng \(20 N/m\) dao động điều hòa dọc theo trục Ox nằm ngang với biên độ \(10 cm\). Khi vật ở vị trí biên thì lực đàn hồi tác dụng lên vật có độ lớn là
Con lắc lò xo nằm ngang, ở vị trí biên, độ lớn lực đàn hồi cực đại: \(F = kA= 2 (N)\)
Một con lắc lò xo gồm vật nhỏ và lò xo nhẹ có độ cứng k, dao động điều hòa dọc theo trục Ox quanh vị trí cân bằng O. Biểu thức lực kéo về tác dụng lên vật theo li độ x là
Biểu thức tính lực kéo về của con lắc lò xo \(F = - kx\)
Con lắc lò xo treo thẳng đứng đang dao động điều hòa với biên độ 4 cm. Tỉ số giữa lực đàn hồi lớn nhất và lực đàn hồi khi đi qua vị trí cân bằng là 3. Lấy g = 10 (m/s2). Tần số góc của dao động là
Giả sử ở vị trí cân bằng, lò xo giãn một đoạn ∆l0
Tỉ số giữa lực đàn hồi lớn nhất và lực đàn hồi khi đi qua vị trí cân bằng là:
\(\begin{array}{l}\dfrac{{{F_{dh\max }}}}{{{F_{dh0}}}} = \dfrac{{k\left( {\Delta {l_0} + A} \right)}}{{k\Delta {l_0}}} = 3 \Rightarrow \Delta {l_0} + A = 3\Delta {l_0}\\ \Rightarrow \Delta {l_0} = \dfrac{A}{2} = 2\,\,\left( {cm} \right) = 0,02\,\,\left( m \right)\end{array}\)
Tần số góc của con lắc là:
\(\omega = \sqrt {\dfrac{g}{{\Delta {l_0}}}} = \sqrt {\dfrac{{10}}{{0,02}}} = 10\sqrt 5 \,\,\left( {rad/s} \right)\)
Một con lắc lò xo treo thẳng đứng, lò xo có khối lượng không đáng kể, \(k = 50 N/m\), \(m = 200 g\). Vật đang nằm yên ở vị trí cân bằng thì được kéo thẳng đứng xuống dưới để lò xo dãn \(12 cm\) rồi thả cho nó dao động điều hòa. Lấy \(g = {{\rm{\pi }}^{\rm{2}}}{\rm{ m/}}{{\rm{s}}^{\rm{2}}}\). Thời gian lực đàn hồi tác dụng vào vật ngược chiều với lực phục hồi trong một chu kì là
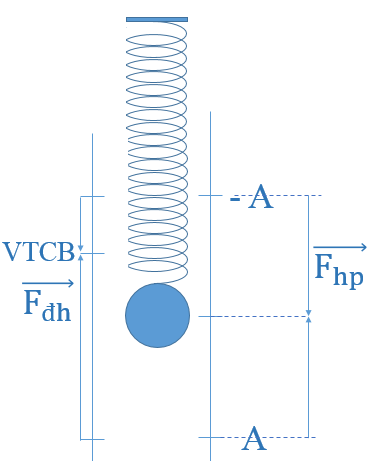
Ta có: \(T = 2\pi \sqrt {\dfrac{{\rm{m}}}{{\rm{k}}}} = 0,{\rm{4 (s)}}\)
Độ biến dạng của lò xo tại vị trí CB là: \(\dfrac{k}{m} = \dfrac{g}{{\Delta l}} \Rightarrow \Delta l = \dfrac{{mg}}{k} = 4(cm)\)
Ta có: \({\rm{\Delta l}} + {\rm{A = 12 (cm)}} \Rightarrow A = 8\) (cm)
Chiều của lực đàn hồi và lực hồi phục được biểu diễn như hình vẽ
\( \Rightarrow \) Thời gian để lực đàn hồi và lực phục hồi ngược chiều nhau là: \(t = 2.\dfrac{T}{{12}} = \dfrac{T}{6} = \dfrac{1}{{15}}\) (s)
Con lắc lò xo gồm vật nhỏ gắn với lò xo nhẹ dao động điều hòa theo phương ngang. Lực kéo về tác dụng vào vật luôn
Lực kéo về tác dụng vào vật luôn hướng về vị trí cân bằng
Một con lắc lò xo dao động theo phương ngang với cơ năng dao động là 20mJ và lực đàn hồi cực đại là 2N. Biên độ dao động của con lắc là
Ta có:
- Cơ năng dao động:
\({\rm{W}} = \dfrac{1}{2}k{A^2} = {20.10^{ - 3}}J\)
- Lực đàn hồi cực đại: Fđhmax = kA = 2N
\( \to \dfrac{{\rm{W}}}{{{F_{{\rm{d}}{{\rm{h}}_{{\rm{max}}}}}}}} = \dfrac{A}{2} = \dfrac{{{{20.10}^{ - 3}}}}{2} \\\to A = 0,02m = 2cm\)
Một con lắc lò xo treo thẳng đứng gồm lò xo có khối lượng không đáng kể . Khi vật nằm cân bằng, lò xo gian một đoạn \(∆l\). Tỉ số giữa lực đàn hồi cực đại và cực tiểu trong quá trình vật dao động là $\dfrac{{{F_{dhmax}}}}{{{F_{dhmin}}}} = a$ . Biên độ dao động của vật được tính bởi biểu thức nào dưới đây ?
Ta có:
- Lực đàn hồi cực đại: Fmax = k(∆l + A)
- Lực đàn hồi cực tiểu: Fmin = k(∆l - A)
$ \to \dfrac{{{F_{dhmax}}}}{{{F_{dhmin}}}} = \dfrac{{\Delta l + A}}{{\Delta l - A}} = a \to A = \dfrac{{\Delta l(a - 1)}}{{a + 1}}$
Một chất điểm có khối lượng \(500 g\) dao động điều hòa dưới tác dụng của một lực kéo về có biểu thức \(F = -0,8cos4t (N)\). Biên độ dao động của chất điểm bằng
Ta có:
\({F_{max}} = kA = m{\omega ^2}A \to A = \dfrac{{{F_{max}}}}{{m{\omega ^2}}} = \dfrac{{0,8}}{{0,{{5.4}^2}}} = 0,1m = 10cm\)
Một con lắc lò xo gồm vật nặng có khối lượng $m$, lò xo có độ cứng k được treo thẳng đứng tại nơi có gia tốc trọng trường là $g$. Kích thích cho con lắc dao động điều hòa theo phương thẳng đứng với biên độ. Khi vật đi qua vị trí cân bằng thì lực đàn hồi của lò xo có độ lớn :
Ta có, tại vị trí cân bằng, lò xo dãn một đoạn \(\Delta l = \dfrac{{mg}}{k}\)
=> Lực đàn hồi, tại vị trí cân bằng:
\(\left| {{F_{dh}}} \right| = k\Delta l = k\dfrac{{mg}}{k} = mg\)
Một con lắc lò xo treo thẳng đứng được kích thích cho dao động điều hòa. Thời gian quả cầu đi từ vị trí cao nhất đến vị trí thấp nhất là 0,15s và tỉ số giữa độ lớn của lực đàn hồi lò xo và trọng lượng quả cầu gắn ở đầu con lắc khi nó ở vị trí thấp nhất là 1,8. Lấy g = π2 m/s2. Biên độ dao động của con lắc là:
(Chọn chiều dương hướng xuống)
Thời gian quả cầu đi từ vị trí cao nhất đến vị trí thấp nhất tương ứng với thời gian đi từ - A đến A và bằng: \(\Delta t = \frac{T}{2} = 0,15{\rm{s}} \to T = 0,3{\rm{s}}\)
- Độ dãn của lò xo tại vị trí cân bằng: \(\Delta l = \frac{{mg}}{k}\)
Vị trí lò xo ở vị trí thấp nhất là x = +A
Từ đầu bài, ta có:
\(\begin{array}{l}\frac{{{F_{dh(x = + A)}}}}{{mg}} = 1,8 = \frac{{k(\Delta l + A)}}{{mg}} = \frac{{k(\frac{{mg}}{k} + A)}}{{mg}} = 1 + \frac{{kA}}{{mg}} = 1 + \frac{{m{\omega ^2}A}}{{mg}} = 1 + \frac{{{\omega ^2}A}}{g}\\ \to \frac{{{\omega ^2}A}}{g} = 0,8 \to A = \frac{{0,8g}}{{{\omega ^2}}} = \frac{{0,8.10}}{{{{\left( {\frac{{20\pi }}{3}} \right)}^2}}} = 0,018m = 1,8cm\end{array}\)
Một con lắc lò xo treo thẳng đứng với biên độ \(8cm\). Khoảng thời gian từ lúc lực đàn hồi cực đại đến lúc lực đàn hồi cực tiểu là \(\dfrac{T}{3}\), với \(T\) là chu kì dao động của con lắc. Tốc độ của vật nặng khi nó cách vị trí thấp nhất \(2cm\). Lấy\(g = {\pi ^2}\left( {m/{s^2}} \right)\).
Chọn chiều dương hướng xuống
Vị trí lực đàn hồi cực đại: \(x = + A\)
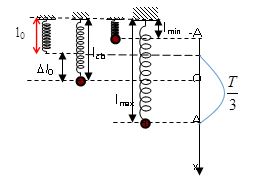
Ta có thời gian từ lúc lực đàn hồi cực đại đến lúc lực đàn hồi cực tiểu là \(\dfrac{T}{3}\)
=> Ta có góc quét: \(\Delta \varphi = \omega \Delta T = \dfrac{{2\pi }}{T}.\dfrac{T}{3} = \dfrac{{2\pi }}{3}\), vẽ trên vòng tròn lượng giác, ta được:
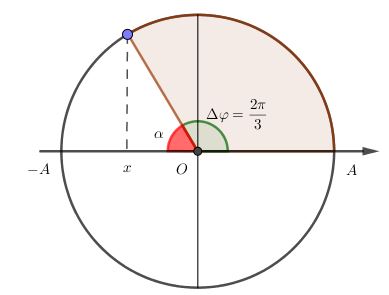
Ta có góc \(\alpha = \pi - \dfrac{{2\pi }}{3} = \dfrac{\pi }{3}\)
=> vị trí lực đàn hồi cực tiểu là \(x = - \Delta l = - Acos\alpha = - Acos\dfrac{\pi }{3} = - \dfrac{A}{2} = - 4cm\)
\( \to \Delta l = \dfrac{{mg}}{k} = \dfrac{{mg}}{{m{\omega ^2}}} = 0,04 \to \omega = \sqrt {\dfrac{g}{{0,04}}} = 5\pi (ra{\rm{d}}/s)\)
- Vị trí cách vị trí thấp nhất \(2cm\) có li độ: \(x{\rm{ }} = {\rm{ }}6cm\)
\({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} \leftrightarrow {8^2} = {6^2} + \dfrac{{{v^2}}}{{{{\left( {5\pi } \right)}^2}}} \to v = \pm 10\sqrt 7 \pi cm/s\)
Con lắc lò xo treo thẳng đứng, dao động điều hòa: \(x = 2cos20t (cm)\). Chiều dài tự nhiên của lò xo là \(l_0= 30cm\), lấy \(g = 10m/s^2\). Chiều dài nhỏ nhất và lớn nhất của lò xo trong quá trình dao động lần lượt là:
Từ phương trình dao động, ta có:
+ Biên độ dao động: \(A = 2cm\)
+ Tần số góc: \(ω = 20 (rad/s)\)
Độ dãn của lò xo tại vị trí cân bằng:
\(\Delta l = \dfrac{{mg}}{k} = \dfrac{{mg}}{{m{\omega ^2}}} = \dfrac{g}{{{\omega ^2}}} = \dfrac{{10}}{{20{}^2}} = 0,025m = 2,5cm\)
+ Chiều dài cực đại của lò xo:
\({l_{{\rm{max}}}} = {l_0} + \Delta {l_0} + A = 30 + 2,5 + 2 = 34,5cm\)
+ Chiều dài cực tiểu của lò xo:
\({l_{{\rm{min}}}} = {l_0} + \Delta {l_0} - A = 30 + 2,5 - 2 = 30,5cm\)
Một lò xo độ cứng \(k = 50 N/m\), một đầu cố định, đầu còn lại treo vật nặng khối lượng \(m = 100g\). Điểm treo lò xo chịu được lực tối đa không quá \(4 N\). Lấy \(g = 10m/s^2\). Để hệ thống không bị rơi thì vật nặng dao động theo phương thẳng đứng với biên độ không quá
Để hệ thống không bị rơi, => lực đàn hồi cực đại ≤ \(4N\)
\( \to {F_{d{h_{{\rm{max}}}}}} = k(\Delta l + A) \le 4N \leftrightarrow k(\dfrac{{mg}}{k} + A) \le 4 \leftrightarrow mg + kA \le 4 \to A \le \dfrac{{4 - 0,1.10}}{{50}} = 0,06m = 6cm\)
Một con lắc lò xo dao động điều hòa theo phương thẳng đứng với chu kì $0,4s$ và biên độ $8cm$. lấy $g = 10 m/s^2$ và \({\pi ^2} \approx 10\). Khoảng thời gian ngắn nhất giữa hai lần công suất tức thời của lực đàn hồi bằng $0$ là:
Chọn chiều dương hướng xuống, ta có:
Độ dãn của lò xo tại vị trí cân bằng:
\(\Delta l = \dfrac{{mg}}{k} = \dfrac{{mg}}{{m{\omega ^2}}} = \dfrac{g}{{{{\left( {\dfrac{{2\pi }}{T}} \right)}^2}}} = \dfrac{{10}}{{{{\left( {\dfrac{{2\pi }}{{0,4}}} \right)}^2}}} = 0,04m = 4cm\)
Lực đàn hồi tại vị trí bất kì:
\({F_{dh}} = k(\Delta l + x)\)
Công suất tức thời: \(P = \left| {Fv} \right| = k\left| {(\Delta l + x)v} \right|\)
Ta có: P = 0 khi \(\left[ \begin{array}{l}x = - \Delta l = - 4cm\\v = 0 \to x = \pm A\end{array} \right.\)
Vẽ vòng tròn lượng giác, ta được:
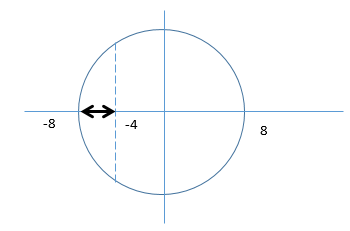
=> Khoảng thời gian ngắn nhất giữa hai lần công suất tức thời của lực đàn hồi bằng $0$ chính bằng khoảng thời gian đi từ $-4cm$ đến $-8cm$ hoặc ngược lại. Khoảng thời gian đó là: \(\Delta t = \dfrac{T}{6} = \dfrac{{0,4}}{6} = \dfrac{1}{{15}}s\)
Con lắc lò xo dao động trên mặt phẳng nằm nghiêng góc α = 300 có độ cứng 50N/m, biên độ 6cm. Biết vật nặng có khối lượng 200g và lấy g = 10m/s2. Hướng và độ lớn lực đàn hồi của lò xo tác dụng vào điểm treo vật của lò xo khi vật đi qua VTCB.
Độ dãn của lò xo tại vị trí cân bằng là: \(\Delta l = \frac{{mg\sin \alpha }}{k} = \frac{{0,2.10.\sin {{30}^0}}}{{50}} = 0,02m = 2cm\)
Lực đàn hồi tại VTCB: Fđh = - k.∆l = - 50. 0,02 = 1N
Tại vị trí cân bằng, lò xo đang dãn => lực đàn hồi có hướng chống lại sự dãn => lực đàn hồi hướng lên
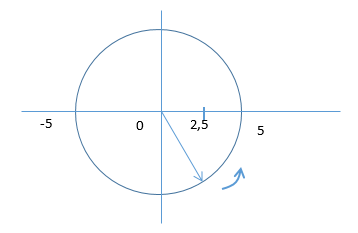
Một con lắc lò xo nằm ngang dao động theo phương trình x = 5cos(2πt - π/3)(cm) ( x tính bằng cm; t tính bằng s). Kể từ t = 0, lực đàn hồi đổi chiều lần đầu tại thời điểm:
Từ phương trình dao động, ta có chu kì dao động: \(T = \dfrac{{2\pi }}{\omega } = 1{\rm{s}}\)
Tại t = 0: \(\left\{ \begin{array}{l}{x_0} = 5c{\rm{os}}\left( { - \dfrac{\pi }{3}} \right) = 2,5cm\\v = - A\omega \sin \left( { - \dfrac{\pi }{3}} \right) > 0\end{array} \right.\)
Lực đàn hồi đổi chiều tại vị trí cân bằng
Từ vòng tròn lượng giác,
=> Lực đàn hồi đổi chiều lần đầu kể từ t = 0 tại thời điểm: \(t = \dfrac{T}{6} + \dfrac{T}{4} = \dfrac{{5T}}{{12}} = \dfrac{5}{{12}}s\)
Một vật dao động theo phương trình \(x = 20\cos (5\pi t/3 - \pi /6)\) cm. Kể từ lúc \(t = 0\) đến lúc vật đi qua vị trí \(x = -10 cm\) lần thứ \(2015\) theo chiều âm thì lực hồi phục sinh công dương trong thời gian:
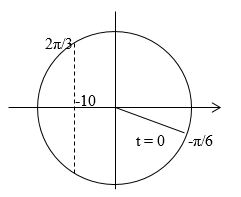
Lực hồi phục luôn luôn hướng về VTCB, lực hồi phục sinh công dương khi vật chuyển động về VTCB và sinh công âm khi chuyện động ra VT biên.
Trong một chu kì, một nửa thời gian (T/2) lực hồi phục sinh công âm, một nửa thời gian (T/2) sinh công dương.
Dựa vào VTLG ta xác định được:
+ Lần 1, vật qua li độ x = -10 cm theo chiều âm ứng với góc quét từ \( - \pi /6\) đến \(2\pi /3\). Trong giai đoạn này khoảng thời gian sinh công dương là T/4 ( ứng với cung phần tư thứ nhất).
+ Để đến thời điểm lần thứ 2015, vật qua li độ x = -10 cm theo chiều âm thì cần quét thêm 2014 vòng và thời gian sinh công dương có thêm là 2014.T/2 = 1007T.
=> Tổng thời gian: T/4 + 1007T = 1208,7 s.
Một con lắc lò xo gồm vật nhỏ nặng 500g gắn với lò xo độ cứng 50N/m đặt trên mặt phẳng ngang nhẵn. Từ vị trí cân bằng truyền cho vật một vận tốc 1m/s dọc theo trục lò xo để vật dao động điều hòa. Công suất cực đại của lực đàn hồi lò xo trong quá trình dao động bằng:
Tần số góc của vật là :
\(\omega = \sqrt {\frac{k}{m}} = \sqrt {\dfrac{{50}}{{0,5}}} = 10rad\)
Tại VTCB truyền vận tốc cho vật
\( \Rightarrow {v_{\max }} = \omega .A \Rightarrow A = \dfrac{{{v_{m{\rm{ax}}}}}}{\omega } = \dfrac{1}{{10}} = 0,1m\)
Công suất của lực đàn hồi: $P = F.v = kx.v$
\({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} \ge \dfrac{2}{\omega }\left| {xv} \right| \Rightarrow \left| {xv} \right| \le \dfrac{{\omega {A^2}}}{2}\)
\({P_{m{\rm{ax}}}} = \dfrac{{k{A^2}\omega }}{2}\)
Dấu bằng xảy ra khi \({x^2} = \dfrac{{{v^2}}}{{{\omega ^2}}}\)
=> Công suất của lực đàn hồi đạt cực đại khi \(x = \dfrac{A}{{\sqrt 2 }},v = \omega \dfrac{A}{{\sqrt 2 }}\)
Công suất cực đại là : \( \Rightarrow P = F.v = k.\dfrac{A}{{\sqrt 2 }}.\dfrac{{\omega A}}{{\sqrt 2 }} = k\omega \dfrac{{{A^2}}}{2} = 2,5W\)
Hai con lắc lò xo nằm ngang dao động điều hòa dọc theo hai đường thẳng song song kề nhau và song song với trục Ox. Hai vật nặng có cùng khối lượng. Vị trí cân bằng của hai dao động đều nằm trên một đường thẳng qua gốc tọa độ và vuông góc với trục Ox. Đồ thị (1), (2) lần lượt biểu diễn mối liên hệ giữa lực kéo về Fkv và li độ x của con lắc 1 và con lắc 2. Biết tại thời điểm t, hai con lắc cùng qua vị trí cân bằng theo cùng một chiều. Sau đó một khoảng thời gian ngắn nhất bằng 0,5s con lắc 1 có động năng bằng một nửa cơ năng của nó, thì thế năng của con lắc 2 khi đó có giá trị gần nhất với giá trị nào sau đây?
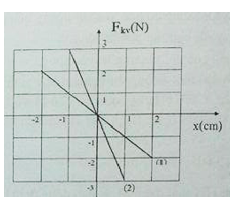
+ Từ đồ thị ta thu được các dữ kiện sau:
* CLLX1 có biên độ dao động A1 = 2cm, lực kéo về cực đại F1max = 2 N => độ cứng của lò xo 1 là k1 = 100 N/m
* CLLX2 có biên độ dao động A2 = 1 cm, lực kéo về cực đại F2max = 3 N => độ cứng của lò xo 2 là k2 = 300 N/m
+ Theo đề bài, tại thời điểm ban đầu, cả hai con lắc đều đi qua VTCB theo một chiều, ở đây giả sử theo chiều dương.
+ Sau thời gian ngắn nhất t = 0,5 thì CLLX1 qua vị trí có động năng bằng nửa cơ năng, tức là VT \({x_1} = \frac{{{A_1}}}{{\sqrt 2 }}\) => thời gian t = T1/8 => T1 = 8t = 8.0,5 = 4 s
Và động năng khi đó của con lắc là \({{\rm{W}}_d} = \frac{{{{\rm{W}}_1}}}{2}{\rm{ = }}\frac{1}{2}\frac{{{k_1}{A_1}^2}}{2} = 0,01(J)\)
+ Ta có \(\frac{{{T_2}}}{{{T_1}}} = \sqrt {\frac{{{k_1}}}{{{k_2}}}} = \frac{1}{{\sqrt 3 }} = > {T_2} = \frac{4}{{\sqrt 3 }}(s)\) => Sau thời gian t = 0,5s =>\(t = \frac{{\sqrt 3 {T_2}}}{8}\) => Khi đó CLLX 2 đang ở vị trí có li độ x2 = 0,98 cm
=> Thế năng của con lắc 2 là: \({{\rm{W}}_{t2}} = \frac{{{k_2}.x_2^2}}{2} = \frac{{300.0,{{98}^2}}}{2} = 0,0144(J)\)
Cơ năng của con lắc 2 là: \({\rm{W}} = \frac{1}{2}{k_2}A_2^2 = \frac{1}{2}.300.0,{01^2} = 0,015\)
Do đó \(\frac{{{{\rm{W}}_{t2}}}}{{\rm{W}}} = 0,96\)

