Một con lắc lò xo treo thẳng đứng, lò xo có khối lượng không đáng kể, \(k = 50 N/m\), \(m = 200 g\). Vật đang nằm yên ở vị trí cân bằng thì được kéo thẳng đứng xuống dưới để lò xo dãn \(12 cm\) rồi thả cho nó dao động điều hòa. Lấy \(g = {{\rm{\pi }}^{\rm{2}}}{\rm{ m/}}{{\rm{s}}^{\rm{2}}}\). Thời gian lực đàn hồi tác dụng vào vật ngược chiều với lực phục hồi trong một chu kì là
Trả lời bởi giáo viên
Ta có: \(T = 2\pi \sqrt {\dfrac{{\rm{m}}}{{\rm{k}}}} = 0,{\rm{4 (s)}}\)
Độ biến dạng của lò xo tại vị trí CB là: \(\dfrac{k}{m} = \dfrac{g}{{\Delta l}} \Rightarrow \Delta l = \dfrac{{mg}}{k} = 4(cm)\)
Ta có: \({\rm{\Delta l}} + {\rm{A = 12 (cm)}} \Rightarrow A = 8\) (cm)
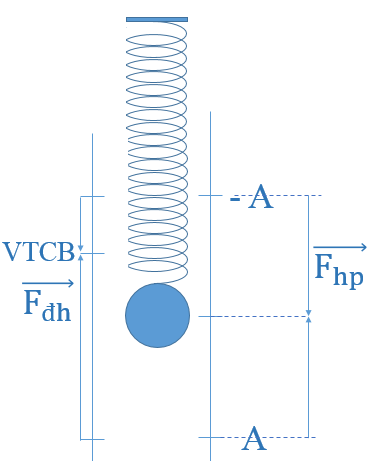
Chiều của lực đàn hồi và lực hồi phục được biểu diễn như hình vẽ
\( \Rightarrow \) Thời gian để lực đàn hồi và lực phục hồi ngược chiều nhau là: \(t = 2.\dfrac{T}{{12}} = \dfrac{T}{6} = \dfrac{1}{{15}}\) (s)
Hướng dẫn giải:
Áp dụng: Lực hồi phục có công thức \({F_{hp}} = - kx\)
Lực đàn hồi có chiều chống lại sự biến dạng của lò xo.

