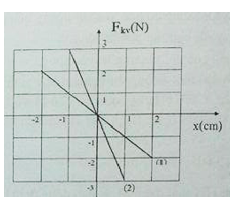
Hai con lắc lò xo nằm ngang dao động điều hòa dọc theo hai đường thẳng song song kề nhau và song song với trục Ox. Hai vật nặng có cùng khối lượng. Vị trí cân bằng của hai dao động đều nằm trên một đường thẳng qua gốc tọa độ và vuông góc với trục Ox. Đồ thị (1), (2) lần lượt biểu diễn mối liên hệ giữa lực kéo về F_kv và li độ x của con lắc 1 và con lắc 2. Biết tại thời điểm t, hai con lắc cùng qua vị trí cân bằng theo cùng một chiều. Sau đó một khoảng thời gian ngắn nhất bằng 0,5s con lắc 1 có động năng bằng một nửa cơ năng của nó, thì thế năng của con lắc 2 khi đó có giá trị gần nhất với giá trị nào sau đây?

 

Chọn phát biểu đúng khi nói về lực kéo về tác dụng vào con lắc lò xo dao động điều hòa theo phương ngang?

Một con lắc lò xo dao động theo phương ngang với cơ năng dao động là \(32mJ\) và lực đàn hồi cực đại tác dụng lên vật có độ lớn là \(4N\). Biên độ dao động của con lắc là:

Một con lắc lò xo treo thẳng đứng gồm lò xo có khối lượng không đáng kể . Khi vật nằm cân bằng, lò xo gian một đoạn \(\Delta l\). Tỉ số giữa lực đàn hồi cực đại và cực tiểu trong quá trình vật dao động là \(\dfrac{{{F_{dh\min }}}}{{{F_{dhmax}}}} = a\) . Biên độ dao động của vật được tính bởi biểu thức nào dưới đây ?

Một chất điểm có khối lượng \(250g\) dao động điều hòa dưới tác dụng của một lực kéo về có biểu thức \(F =  - 0,75cos\left( {4t} \right)N\). Biên độ dao động của chất điểm bằng

Một con lắc lò xo gồm vật nặng có khối lượng \(m\), lò xo có độ cứng \(k\) được treo thẳng đứng tại nơi có gia tốc trọng trường là \(g\). Kích thích cho con lắc dao động điều hòa theo phương thẳng đứng với biên độ. Khi vật đi qua vị trí biên dương thì lực đàn hồi của lò xo có độ lớn :

Một con lắc lò xo treo thẳng đứng được kích thích cho dao động điều hòa. Thời gian quả cầu đi từ vị trí cao nhất đến vị trí thấp nhất là \(0,02s\) và tỉ số giữa độ lớn của lực đàn hồi lò xo và trọng lượng quả cầu gắn ở đầu con lắc khi nó ở vị trí thấp nhất là \(6\). Lấy \(g = {\pi ^2} = 10m/{s^2}\). Biên độ dao động của con lắc là:

Một con lắc lò xo treo thẳng đứng với biên độ \(A = 10cm\). Khoảng thời gian từ lúc lực đàn hồi cực đại đến lúc lực đàn hồi cực tiểu là \(\dfrac{T}{3}\), với \(T\) là chu kì dao động của con lắc. Tốc độ của vật nặng khi nó cách vị trí thấp nhất \(4cm\) có giá trị là bao nhiêu? Lấy \(g = {\pi ^2} = 10m/{s^2}\)