Sóng dừng

+ Ta có điều kiện để có sóng dừng trên dây hai đầu cố định: $l = k\frac{\lambda }{2}{\rm{  }}(k \in {N^*})$  (k = số bụng sóng)

+ Có 2 bụng sóng khi $k = 2 \to l = 2\frac{\lambda }{2} = \lambda$

+ Ta có điều kiện để có sóng dừng trên dây hai đầu cố định: $l = k\dfrac{\lambda }{2}{\rm{  }}(k \in {N^*})$

+ Theo đề bài ta có : Số bụng sóng = số bó sóng = k = 2

$l = 2\dfrac{\lambda }{2} = 2\dfrac{v}{{2f}} \to f = \dfrac{v}{l}$

+ Điều kiện để có sóng dừng trên dây hai đầu cố định: $l = k\frac{\lambda }{2}{\rm{  }}(k \in {N^*})$

Số bụng sóng = số bó sóng = k ;   Số nút sóng = k + 1

Ta có, chiều dài dây : $l = k\frac{\lambda }{2} = k\frac{v}{{2f}}$

+ Khi trên dây có 5 điểm nút ứng với 4 điểm bụng: $l = 4\frac{v}{{2f}}$      (1)

+ Khi trên dây có 5 điểm bụng: $l = 5\frac{v}{{2f'}}$             (2)

Lấy $\frac{{\left( 1 \right)}}{{\left( 2 \right)}}$ ta được: $\frac{{4\frac{v}{{2f}}}}{{5\frac{v}{{2f'}}}} = 1 \to f' = \frac{5}{4}f = \frac{5}{4}.50 = 62,5Hz$

+ Khi B tự do thì: $l = \left( {2k + 1} \right)\dfrac{{{\lambda _1}}}{4} = \left( {2k + 1} \right)\dfrac{v}{{4{f_1}}}$

Trên dây có 5 bụng sóng ứng với $k = 4$ , ta suy ra: $l = \left( {2.4 + 1} \right)\dfrac{v}{{4{f_1}}} = 9\dfrac{v}{{4{f_1}}}$  (1)

+ Khi B cố định thì: $l = k'\dfrac{{{\lambda _2}}}{2} = k'\dfrac{v}{{2{f_2}}}$

Trên dây có 5 nút sóng ứng với $k' = 4$, ta suy ra: $l = 4\dfrac{v}{{2{f_2}}}$  (2)

Từ (1) và (2) ta suy ra: $9\dfrac{v}{{4{f_1}}} = 4\dfrac{v}{{2{f_2}}} \to {f_2} = \dfrac{8}{9}{f_1} = \dfrac{8}{9}.18 = 16Hz$

+ Ta có, bước sóng: $\lambda  = \dfrac{v}{f} = \dfrac{{16}}{{50}} = 0,32{\rm{ }}m = 32cm$

+ Ta có điều kiện để có sóng dừng trên dây hai đầu cố định: $l = k\dfrac{\lambda }{2}{\rm{  }}(k \in {N^*})$

Số bụng sóng = số bó sóng = k ; Số nút sóng = k + 1

Trên dây có: $k = \dfrac{l}{{\dfrac{\lambda }{2}}} = \dfrac{{2l}}{\lambda } = \dfrac{{2.80}}{{32}} = 5$ bụng sóng.

=> Số nút = k + 1 = 6 nút sóng

+ Ta có điều kiện để có sóng dừng trên dây hai đầu cố định: $l = k\frac{\lambda }{2}{\rm{  }}(k \in {N^*})$

Số bụng sóng = số bó sóng = k ; Số nút sóng = k + 1

$l = k\frac{\lambda }{2} \leftrightarrow 1,2 = 9\frac{\lambda }{2} \to \lambda  = 0,4m$

+ Tốc độ truyền sóng trên dây: $v = \lambda f = 0,4.60 = 24m/s$

+ Ta có, bước sóng:  $\lambda  = \frac{v}{f} = \frac{{60}}{{50}} = 1,2{\rm{ }}cm$

+ Ta có điều kiện để có sóng dừng trên dây hai đầu cố định: $l = k\frac{\lambda }{2}{\rm{  }}(k \in {N^*})$

Số bụng sóng = số bó sóng = k ; Số nút sóng = k + 1

AM = 5$\frac{\lambda }{2}$ = 3 cm

=> M là nút số 6

$l = k\frac{\lambda }{2}{\rm{ }} \leftrightarrow 60 = {\rm{k}}\frac{{1,2}}{2} \to k = 100$

=> Trên dây có 100 bụng, 101 nút

+ Ta có điều kiện để có sóng dừng trên dây hai đầu cố định: $l = k\frac{\lambda }{2}{\rm{  }}(k \in {N^*})$

Số bụng sóng = số bó sóng = k ; Số nút sóng = k + 1

$l = k\frac{\lambda }{2} = k\frac{v}{{2f}} \to f = \frac{{kv}}{{2l}}$

+ Khi trên dây có 5 nút sóng,$k{\rm{ }} = {\rm{ }}4$: ${f_1} = \frac{{4v}}{{2l}}$

+ Khi trên dây có 3 bụng sóng, $k = 3$: ${f_2} = \frac{{3v}}{{2l}}$

$\begin{array}{l} \to \frac{{{f_1}}}{{{f_2}}} = \frac{4}{3} \to {f_2} = \frac{3}{4}{f_1} = \frac{3}{4}.16 = 12H{\rm{z}}\\ \to {f_2} - {f_1} = 12 - 16 =  - 4H{\rm{z}}\end{array}$

=> Giảm tần số đi 4Hz

+ Ta có, bước sóng:  $\lambda  = \frac{v}{f} = \frac{{330}}{{137,5}} = 2,4m$

+ Đầu kín của ống sáo là nút, đầu hở là bụng của sóng dừng nên chiều dài của ống sáo là: $l = (2k + 1)\frac{\lambda }{4}{\rm{  }}(k \in N)$

Với số bó (bụng) sóng nguyên = k; Số bụng sóng = số nút sóng = k + 1

Ta có, âm trong sao dao động với tần số cơ bản $80Hz$ ứng với 1 bụng sóng hay $k = 0$

=> chiều dài ống sáo: $l = \frac{\lambda }{4} = \frac{{2,4}}{4} = 0,6m$

Ta có: ${A_M} = 2A\left| {{\rm{cos}}(2\pi \frac{d}{\lambda })} \right| = a\left| {{\rm{cos}}(2\pi \frac{d}{\lambda })} \right|$

Tại điểm cách bụng sóng một phần ba bước sóng có:

$d = \frac{\lambda }{3} \to {A_M} = a\left| {{\rm{cos}}(2\pi \frac{1}{3})} \right| = \frac{a}{2}$

+ Vì B là điểm bụng gần nút A nhất

C- là trung điểm của AB

=> $AC = \frac{\lambda }{8} = 9cm \to \lambda  = 72cm$

+ Biên độ dao động của phần tử tại C: ${A_C} = 2A\left| {{\rm{cos}}(2\pi \frac{d}{\lambda })} \right| = 2A\left| {{\rm{cos}}(2\pi \frac{{\frac{\lambda }{8}}}{\lambda })} \right| = A\sqrt 2$

+ Khoảng thời gian ngắn nhất giữa hai lần mà li độ dao động của phần tử tại B bằng biên độ dao động của phần tử tại C là: $\frac{T}{4} = 0,4{\rm{s}} \to T = 1,6{\rm{s}}$

+ Vận tốc truyền sóng: $v = \frac{\lambda }{T} = \frac{{0,72}}{{1,6}} = 0,45m/s = 45cm/s$

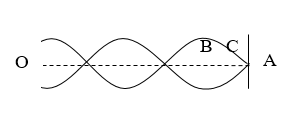
+ Giả sử biểu thức sóng tại nguồn O (cách A: OA = l) $u = acos\omega t$

Xét điểm C cách A:   CA = d. Biên độ của sóng dừng tai C:  ${a_C} = 2asin\frac{{2\pi d}}{\lambda }$

Biên độ của B: ${a_B} = 2a$

Để ${a_C} = a$ (bằng nửa biện độ của B là bụng sóng):  $sin\frac{{2\pi d}}{\lambda } = 0,5 \to \frac{{2\pi d}}{\lambda } = \frac{\pi }{6} + k2\pi$

$\to d = (\frac{1}{{12}} + {\rm{ }}k)\lambda$

Mặt khác: $AB = \frac{\lambda }{4} = 12cm \to \lambda  = 48cm$

Điểm C gần A nhất ứng với $k{\rm{ }} = {\rm{ }}0$

$\to d = AC = \frac{\lambda }{{12}} = \frac{{48}}{{12}} = 4cm$

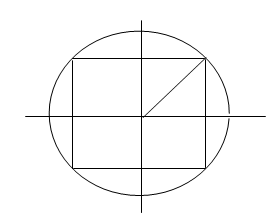
Các điểm dao động với biên độ $b \ne 0$ và $b \ne 2a$ (tức là không phải là điểm nút và điểm bụng) cách đều nhau thì khoảng cách giữa hai điểm bằng $\frac{\lambda }{4} = 0,6m \to \lambda  = 2,4m$

Do đó: $v = \lambda f = \lambda .\frac{\omega }{{2\pi }} = 2,4.\frac{{50}}{{2\pi }} = 60m/s$

Theo hình vẽ ta thấy: $b = \frac{{2a\sqrt 2 }}{2} = a\sqrt 2$

 (Biên độ của bụng sóng là 2a)

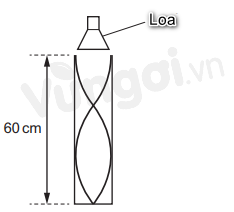
Từ hình vẽ ta có chiều dài cột không khí là: $l = 60cm = 0,6m$

Sóng dừng được hình thành với hai nút và hai bụng nên:

$l = \dfrac{\lambda }{2} + \dfrac{\lambda }{4} \Leftrightarrow l = \dfrac{{3\lambda }}{4} = \dfrac{{3v}}{{4.f}} \Rightarrow f = \dfrac{{3v}}{{4.l}}$

Thay số ta được: $f = \dfrac{{3.340}}{{4.0,6}} = 425Hz$

Nhận xét: hai điểm M, N thuộc hai bó sóng liền kề → M, N dao động ngược pha

Áp dụng công thức độc lập với thời gian cho 2 điểm M, N tại haia thời điểm t₁, t₂, ta có:

$\begin{array}{l}\left\{ \begin{array}{l}\dfrac{{{u_{1M}}}}{{{A_M}}} =  - \dfrac{{{u_{1N}}}}{{{A_N}}}\\\dfrac{{{u_{2M}}}}{{{A_M}}} =  - \dfrac{{{u_{2N}}}}{{{A_N}}}\end{array} \right. \Rightarrow \dfrac{{\left| {{u_{1M}} - {u_{2M}}} \right|}}{{{A_M}}} = \dfrac{{\left| {{u_{1N}} - {u_{2N}}} \right|}}{{{A_N}}}\\ \Rightarrow \dfrac{{{M_1}{M_2}}}{{{A_M}}} = \dfrac{{{N_1}{N_2}}}{{{A_N}}} \Rightarrow \dfrac{{{M_1}{M_2}}}{{{N_1}{N_2}}} = \dfrac{{{A_M}}}{{{A_N}}}\end{array}$

Biên độ của hai điểm M, N là:

$\begin{array}{l}\left\{ \begin{array}{l}{A_M} = 2A\left| {\sin \dfrac{{2\pi {x_M}}}{\lambda }} \right|\\{A_N} = 2A\left| {\sin \dfrac{{2\pi {x_N}}}{\lambda }} \right|\end{array} \right. \Rightarrow \dfrac{{{A_M}}}{{{A_N}}} = \dfrac{{\left| {\sin \dfrac{{2\pi {x_M}}}{\lambda }} \right|}}{{\left| {\sin \dfrac{{2\pi {x_N}}}{\lambda }} \right|}}\\ \Rightarrow \dfrac{{{M_1}{M_2}}}{{{N_1}{N_2}}} = \dfrac{{{A_M}}}{{{A_N}}} = \dfrac{{\left| {\sin \dfrac{{2\pi .20}}{{50}}} \right|}}{{\left| {\sin \dfrac{{2\pi .35}}{{50}}} \right|}} \approx 0,618\end{array}$

Ta có: Đầu B tự do và A cố định

$AB = \dfrac{{\left( {2k + 1} \right)\lambda }}{4}$ với số bụng sóng bằng (k + 1)

=> Muốn có 8 bụng sóng tức là $k=7$ thì

$\Rightarrow \lambda  = \dfrac{{4.AB}}{{\left( {2k + 1} \right)}} = \dfrac{{4.AB}}{{{15}}} = 5,6{\rm{ (cm)}} \\\Rightarrow f = \dfrac{v}{\lambda } = \dfrac{4}{{5,{{6.10}^{ - 2}}}} = 71,{\rm{4 (Hz)}}$

Ta có, sóng dừng trên dây 2 đầu cố định, chiều dài dây khi đó: $l = k\frac{\lambda }{2}$

Thay $\left\{ \begin{array}{l}\lambda  = 40cm\\k = 5\end{array} \right.$ vào ta được: $l = 5\frac{{40}}{2} = 100cm$

Trong sóng dừng có một số điểm luôn luôn đứng yên gọi là nút, và một số điểm luôn luôn dao động với biên độ cực đại gọi là bụng.

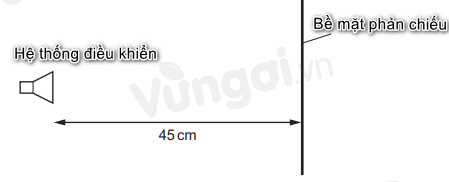
Ta có: $\left\{ \begin{array}{l}l = 45cm = 0,45m\\v = c = {3.10^8}m/s\\f = 1GHz = {10^9}Hz\end{array} \right.$

Một sóng dừng được tạo ra với một nút tại máy phát và một nút ở bề mặt.

Áp dụng điều kiện có sóng dừng với hai đầu là nút sóng ta có:

$l = \dfrac{{k\lambda }}{2} = \dfrac{{k.v}}{{2f}} \Rightarrow k = \dfrac{{2.l.f}}{v} = \dfrac{{2.0,{{45.10}^9}}}{{{{3.10}^8}}} = 3$

$\Rightarrow$ Có 3 bụng sóng trong không gian giữa máy phát và mặt phản xạ.

Khi có sóng dừng thì trên dây xuất hiện những điểm luôn luôn đứng yên gọi là nút, và một số điểm luôn luôn dao động với biên độ cực đại gọi là bụng.