Trong đoạn mạch AB có ba phần tử R, L, C không phân nhánh, gọi uAB,uR,uL,uC lần lượt là các điện áp tức thời giữa hai đầu đoạn mạch, điện trở R, cuộn dây thuần cảm và tụ điện, i là dòng điện qua đoạn mạch. Chọn phát biểu đúng:
A, C, D - sai
B - đúng
Mắc mạch điện xoay chiều R, L, C nối tiếp vào điện áp u=U0cos(100πt+π2)(V) thì dòng điện qua mạch là i=I0cos(100πt+π6)(A). Kết luận nào sau đây đúng:
Cách 1 :
Ta có :
u=U0cos(100πt+π2)
i=I0cos(100πt+π6)
Độ lệch pha của u so với i :
φ=π2−π6=π3(rad)
Nhận xét, u nhanh pha hơn i => cảm kháng lớn hơn dung kháng
Cách 2 :
Ta có , độ lệch pha giữa u và i được xác định bởi biểu thức :
tanφ=ZL−ZCR
Mặt khác, theo đầu bài ta có :
φ=π2−π6=π3(rad)
tanφ=ZL−ZCR=tanπ3→ZL−ZC=√3R→ZL>ZC
Một mạch điện xoay chiều RLC nối tiếp có UR = 40 V; UL = 50 V; UC = 80 V. Điện áp hai đầu đoạn mạch là:
Điện áp hai đầu đoạn mạch :
U=√U2R+(UL−UC)2=√402+(50−80)2=50(V)
Đoạn mạch RLC nối tiếp. Biết điện áp tức thời ở hai đầu đoạn mạch sớm pha hơn cường độ dòng điện tức thời i chạy qua mạch 450. Chọn kết luận đúng:
Ta có :
+ u nhanh pha hơn i một góc 450
+ độ lệch pha giữa u và i được xác định bởi biểu thức :
tanφ=ZL−ZCR
→tanφ=ZL−ZCR=tanπ4→ZL−ZC=R
Mạch điện xoay chiều RLC nối tiếp. Biết điện áp tức thời giữa hai đầu đoạn mạch chậm pha hơn cường độ dòng điện tức thời là: 600 vàR=10√3Ω;ZL=50Ω. Dung kháng của tụ điện có giá trị là
Ta có, điện áp tức thời giữa hai đầu đoạn mạch chậm pha hơn cường độ dòng điện tức thời góc 600
→φ=−π3
Mặt khác, ta có:
tanφ=ZL−ZCR=tan(−π3)→ZL−ZC=−√3R→ZC=ZL+√3R=50+√3.10√3=80Ω
Mạch RLC nối tiếp có R=100Ω, L và C=200π(μF). Cho biết f=50Hz và dòng điện qua mạch chậm pha 450. Giá trị đúng của L là:
Ta có:
+ Dung kháng :
ZC=1ωC=12πfC=12π.50.200π.10−6=50Ω
+ Dòng điện qua mạch chậm pha
450→φ=π4
tanφ=ZL−ZCR=tanπ4→ZL−ZC=R→ZL=ZC+R=50+100=150Ω
Mặt khác:
ZL=ωL→L=ZLω=ZL2πf=1502π.50=1,5π
Điện áp của mạch điện xoay chiều là u=100√2cos(100πt+π2)V và cường độ dòng điện qua mạch là i=5√2cos(100πt+π3)A. Trong mạch điện có thể có:
Ta có:
u=100√2cos(100πt+π2)V và i=5√2cos(100πt+π3)A
=> Độ lệch pha giữa u và i:
φ=π2−π3=π6>0
Mặt khác, ta có:
tanφ=ZL−ZCR
=> Mạch có thể chứa R, L, C trong đó ZL > ZC hoặc mạch chỉ chứa R và L
Một mạch điện xoay chiều gồm R và L nối tiếp. Điện áp ở hai đầu đoạn mạchu=100√2cos(100πt+π2)V và cường độ dòng điện qua mạch là i=5cos(100πt+π4)A. Giá trị của R và L là:
Ta có:
u=100√2cos(100πt+π2)V và i=5cos(100πt+π4)A
Độ lệch pha của u so với i:
φ=π2−π4
Lại có:
tanφ=ZL−ZCR
Vì mạch chỉ gồm R, L => ZC = 0
→tanφ=ZLR=tanπ4→ZL=R
Mặt khác, tổng trở của mạch:
Z=U0I0=100√25=20√2Ω
Lại có:
Z=√R2+(ZL)2=√2R=√2ZL=20√2→{R=20ΩZL=20Ω→L=ZLω=20100π=15πH
Đoạn mạch RLC nối tiếp R=40Ω; L=0,4π(H) và C=10−3π(F). Cho tần số dòng điện là 50Hz và điện áp hiệu dụng ở hai đầu R là 80V. Điện áp ở hai đầu đoạn mạch là:
Ta có:
Cường độ dòng điện trong mạch:
I=URR=8040=2(A)
Cảm kháng:
ZL=ωL=2πfL=2π.50.0,4π=40Ω
Hiệu điện thế hiệu dụng hai đầu cuộn cảm:
UL=I.ZL=2.40=80(V)
Dung kháng:
ZC=1ωC=12πfC=12π.50.10−3π=10Ω
Hiệu điện thế hiệu dụng hai đầu tụ điện:
UC=I.ZC=2.10=20(V)
Hiệu điện thế hiệu dụng toàn mạch:
U=√U2R+(UL−UC)2=√802+(80−20)2=100(V)
Đặt vào hai đầu đoạn mạch R, L, C mắc nối tiếp một điện áp xoay chiều u=U0cosωt(V). Kí hiệu UR, UL, UC tương ứng là điện áp hiệu dụng ở hai đầu điện trở thuần R, cuộn dây thuần cảm (cảm thuần) L và tụ điện C. Khi 2√3UR3=2UL=UC thì độ lệch pha giữa cường độ dòng điện so với điện áp giữa hai đầu đoạn mạch là:
Ta có độ lệch pha của điện áp so với cường độ dòng điện trong mạch:
tanφ=ZL−ZCR=UL−UCUR=√33UR−2√33URUR=−√33→φ=−π6
=> u chậm pha hơn i một góc π6
=> i sớm pha hơn u một góc π6
Cho mạch điện xoay chiều như hình vẽ, cuộn dây thuần cảm. Số chỉ các vôn kế V1 , V2 lần lượt là U1 = 80V; U2 = 60V. Biết hiệu điện thế tức thời uAN biến thiên lệch pha π2 với hiệu điện thế tức thời uMB. Hiệu điện thế hiệu dụng ở hai đầu điện trở thuần là:
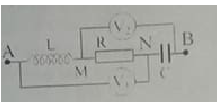
Ta có:
URL⊥URC→|tanφ1tanφ2|=1→ZLRZCR=1→ULUC=U2R
{U2R+U2L=802(1)U2R+U2C=602(2)(1)+(2)↔2U2R+U2L+U2C=802+602↔2U2R+(UL+UC)2−2ULUC=802+602→(UL+UC)=100(1)−(2)↔U2L−U2C=802−602↔(UL+UC)(UL−UC)=802−602→(UL−UC)=28→{UL=64UC=36→UR=√802−642=48V
Một đoạn mạch nối tiếp gồm một cuộn dây và một tụ điện. Hiệu điện thế hiệu dụng hai đầu đoạn mạch, hai đầu cuộn dây, hai đầu tụ điện đều bằng nhau. Hệ số công suất cosφ của đoạn mạch là:
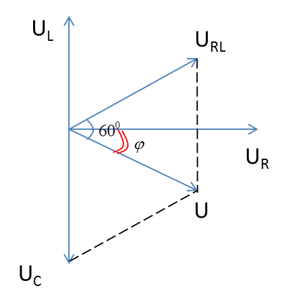
Từ giản đồ véc tơ, ta có:
φ=π−(π3+π2)=π6→cosφ=cosπ6=√32
Một cuộn dây có điện trở thuần r, độ tự cảm L ghép nối tiếp với một tụ điện có điện dung C vào nguồn điện có hiệu điện thế uAB=U√2cos(2πft)V. Ta đo được các hiệu điện thế hiệu dụng hai đầu cuộn dây, hai đầu tụ điện và hai đầu mạch AB là như nhau: Ucd = UC = UAB. Lúc này, góc lệch pha giữa các hiệu điện thế tức thời ucd và uC có giả trị là:
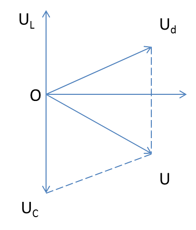
Ta có: Ud = UC = U
=> tứ giác OUdUUC là hình thoi
=> góc lệch pha giữa ud và uc là 1200 = 2π/3
Để xác định độ tự cảm L và điện trở trong r của một cuộn dây, một học sinh mắc nối tiếp điện trở R=10Ω với cuộn dây như hình (hình a). Dùng vôn kế đo các điện áp trên mạch với các vị trí Uab, Ubc, Uac, sau đó giản đồ Frenen với các véc-tơ tương ứng theo đúng tỉ lệ như hình (hình b). Độ tự cảm và điện trở trong của cuộn dây trong thí nghiệm này gần giá trị nào nhất? Biết tần số góc của mạch ω=100π(rad/s)
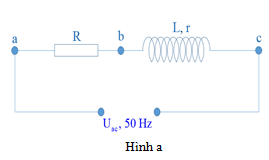
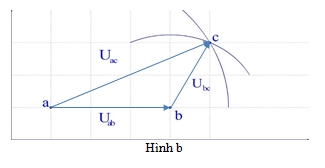
Từ đồ thị ta có:
Ubc=√53Uab⇔Z2L+r2=59R2
Uac=2√53Uab⇔(R+r)2+Z2L=209R2
⇒R2+2Rr+59R2=209R2⇔13R2=Rr⇔r=R3=103(Ω)≈3,3(Ω)
⇔Z2L+R29=59R2⇒ZL=23R=203(Ω)⇒L=ZLω=203.100π=0,021(H)
Mạch điện xoay chiều gồm R, L, C nối tiếp có điện áp hai đầu là u = U0cos(ωt). Độ lệch pha của dòng điện trong mạch so với điện áp đặt vào phụ thuộc vào
Độ lệch pha giữa điện áp hai đầu đoạn mạch và cường độ dòng điện là:
cosφ=R√R2+(ZL−ZC)2=R√R2+(ωL−1ωC)2
→ cosφ phụ thuộc vào R, ω, L, C
Đặt điện áp xoay chiều có biểu thức u=U0cosωt(V) trong đó U0,ω không đổi vào hai đầu đoạn mạch gồm RLC nối tiếp, cuộn dây thuần cảm. Tại thời điểm t1 , điện áp tức thời ở hai đầu RLC lần lượt là uR=50V,uL=30V,uC=−180V . Tại thời điểm t2 các giá trị trên tương ứng là uR=100V,uL=uC=0V . Điện áp cực đại ở hai đầu đoạn mạch là
Tại t2, ta có: {uL=uC=0uR=100V khi này uRmax=U0R=100V
Tại t1, ta có: {uL=30VuC=−180VuR=50V
Ta có: uL⊥uR ta suy ra: (uLU0L)2+(uRU0R)2=1
⇒302U20L+5021002=1⇒U0L=20√3V
Lại có: U0LU0C=ZLZC=−uLuC=−30(−180)=16⇒U0C=120√3V
Điện áp cực đại ở hai đầu mạch: U0=√U20R+(U0L−U0C)2=200V
Đặt điện áp u=220√2cos100πt(V) vào hai đầu đoạn mạch gồm điện trở 20Ω, cuộn cảm thuần có độ tự cảm 0,8πH và tụ điện có điện dung 10−36πF mắc nối tiếp. Khi điện áp tức thời giữa hai đầu điện trở bằng 110√3V thì điện áp tức thời giữa hai đầu cuộn cảm có độ lớn là:
Ta có: {R=20ΩZL=ωL=80ΩZC=1ωC=60Ω⇒Z√R2+(ZL−ZC)2=20√2Ω
Cường độ dòng điện cực đại: I0=U0Z=220√220√2=11A
⇒{U0R=I0.R=11.20=220VU0L=I0.ZL=11.80=880V
Lại có:
u2RU20R+u2LU20L=1⇒|uL|=U0L√1−u2RU20R=880.√(110√3)22202=440V
Đặt điện áp u=U0cos(100πt+π2)V vào hai đầu một mạch điện ghép nối tiếp gồm điện trở thuần, cuộn cảm thuần và tụ điện đều có giá trị khác 0. Pha ban đầu của dòng điện qua mạch (φi) có giá trị
Độ lệch pha giữa u và i: tanφ=ZL−ZCR
Ta có giản đồ vecto:
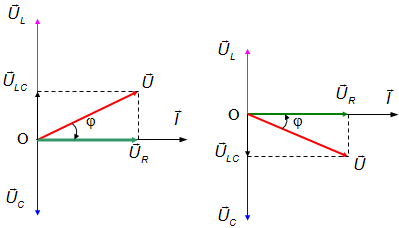
Từ giản đồ vecto ta thấy: −π2<φ<π2
−π2<φu−φi<π2⇔−π2<π2−φi<π2⇔0<φi<π
Đặt điện áp xoay chiềuu=U0cos(100πt)(V) vào hai đầu đoạn mạch nối tiếp gồm điện trở thuần R=100√3Ω , cuộn cảm thuần có độ tự cảm L=2πH và và tụ điện có điện dung C=100πμF . Tại thời điểm khi điện áp tức thời giữa hai đầu đoạn mạch có giá trị bằng một nửa giá trị cực đại thì cường độ dòng điện tức thời trong mạch là √32A . Dùng vôn kế nhiệt có điện trở rất lớn để đo hiệu điện thế hai đầu tụ điện thì vôn kế chỉ
Cảm kháng, dung kháng, tổng trở:
{ZL=ωL=200ΩZC=1ωC=100ΩZ=√R2+(ZL−ZC)2=200Ω
Độ lệch pha giữa u và i:
tanφ=ZL−ZCR=200−100100√3=1√3⇒φ=π6
Khi điện áp bằng nửa giá trị cực đại thì
u=12U0⇔cosφu=12⇒φu=π3⇒φi=φu−φ=π3−π6=π6
Khi đó:
i=I0.cosφi⇒I0=icosφi=√32cosπ6=1A
Số đo của Vôn kế xoay chiều là điện áp hiệu dụng:
UC=I.ZC=I0√2.ZC=1√2.100=50√2V
Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Biết cảm kháng của cuộn cảm bằng 3 lần dung kháng của tụ điện. Tại thời điểm t, điện áp tức thời giữa hai đầu điện trở và điện áp tức thời giữa hai đầu tụ điện có giá trị tương ứng là 60V và 20V. Khi đó, điện áp tức thời giữa hai đầu đoạn mạch là
Ta có: ZL=3ZC⇒uL=−3uC (do uL ngược pha với uC)
Tại thời điểm t: {uR=60VuC=20VuL=−3uC=−60V
Điện áp tức thời giữa hai đầu đoạn mạch khi đó: u=uR+uL+uC=60+(−60)+20=20V

