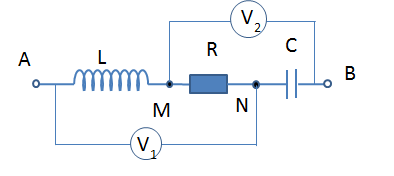
Mạch RLC nối tiếp có \(R = 100\Omega \), L và \(C = \dfrac{{200}}{\pi }(\mu F)\). Cho biết $f = 50 Hz$ và dòng điện qua mạch chậm pha $45^0$. Giá trị đúng của $L$ là:

Đặt điện áp xoay chiều \(u = U\sqrt 2 \cos \omega t\) vào hai đầu đoạn mạch chỉ có tụ điện. Tại thời điểm t₁ , giá trị tức thời của cường độ dòng điện trong đoạn mạch là 2 A và điện áp tức thời giữa hai đầu đoạn mạch bằng 0. Tại thời điểm t₂, giá trị tức thời của cường độ dòng điện trong đoạn mạch là 1 A và điện áp tức thời giữa hai đầu đoạn mạch là \(2\sqrt 3 \,\,V\). Dung kháng của tụ điện là

Đoạn mạch RLC nối tiếp \(R = 40\Omega \); \(L = \dfrac{{0,4}}{\pi }(H)\)và \(C = \dfrac{{{{10}^{ - 3}}}}{\pi }(F)\). Cho tần số dòng điện là \(50{\rm{ }}Hz\) và điện áp hiệu dụng ở hai đầu R là \(40{\rm{ }}V\). Điện áp ở hai đầu đoạn mạch là:

Đặt vào hai đầu đoạn mạch R, L, C mắc nối tiếp một điện áp xoay chiều \(u = {U_0}cos\left( {\omega t + \varphi } \right)V\). Kí hiệu \({U_R},{\rm{ }}{U_L},{\rm{ }}{U_C}\) tương ứng là điện áp hiệu dụng ở hai đầu điện trở thuần \(R\), cuộn dây thuần cảm (cảm thuần)  \(L\) và tụ điện \(C\). Khi \(2\sqrt 3 {U_R} = 2{U_L} = {U_C}\) thì độ lệch pha giữa cường độ dòng điện so với điện áp giữa hai đầu đoạn mạch là:

Cho mạch điện xoay chiều như hình vẽ, cuộn dây thuần cảm. Số chỉ các vôn kế \({V_1},{\rm{ }}{V_2}\) lần lượt là \({U_1} = {\rm{ }}30V\); \({U_2} = 40V\). Biết hiệu điện thế tức thời \({u_{AN}}\) biến thiên lệch pha \(\dfrac{\pi }{2}\) với hiệu điện thế tức thời \({u_{MB}}\). Hiệu điện thế hiệu dụng ở hai đầu điện trở thuần là:

Một đoạn mạch nối tiếp gồm một cuộn dây và một tụ điện. Hiệu điện thế hiệu dụng hai đầu đoạn mạch, hai đầu cuộn dây, hai đầu tụ điện đều bằng nhau. Độ lệch pha của điện áp so với cường độ dòng điện của đoạn mạch là:

Một cuộn dây có điện trở thuần r, độ tự cảm L ghép nối tiếp với một tụ điện có điện dung C vào nguồn điện có hiệu điện thế \({u_{AB}} = U\sqrt 2 {\rm{cos}}\left( {2\pi ft} \right)V\). Ta đo được các hiệu điện thế hiệu dụng hai đầu cuộn dây, hai đầu tụ điện và hai đầu mạch AB là như nhau: . Lúc này, góc lệch pha giữa các hiệu điện thế tức thời \({u_{cd}}\) và \({u_{AB}}\) có giả trị là:

Đặt điện áp xoay vào hai đầu đoạn mạch gồm điện trở thuần \(R = 40\Omega \) mắc nối tiếp với tụ điện thì dung kháng của tụ điện là \({Z_C} = 60\Omega \). Tổng trở của đoạn mạch là