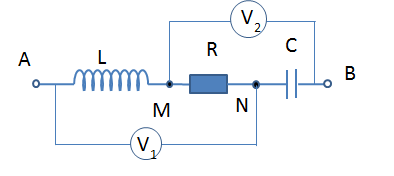
Đặt vào hai đầu đoạn mạch R, L, C mắc nối tiếp một điện áp xoay chiều $u = {U_0}{\rm{cos}}\omega {\rm{t}}(V)$. Kí hiệu UR, UL, UC tương ứng là điện áp hiệu dụng ở hai đầu điện trở thuần R, cuộn dây thuần cảm (cảm thuần) L và tụ điện C. Khi \(\dfrac{{2\sqrt 3 {U_R}}}{3} = 2{U_L} = {U_C}\) thì độ lệch pha giữa cường độ dòng điện so với điện áp giữa hai đầu đoạn mạch là:
Trả lời bởi giáo viên
Ta có độ lệch pha của điện áp so với cường độ dòng điện trong mạch:
\(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R} = \dfrac{{{U_L} - {U_C}}}{{{U_R}}} = \dfrac{{\dfrac{{\sqrt 3 }}{3}{U_R} - \dfrac{{2\sqrt 3 }}{3}{U_R}}}{{{U_R}}} = - \dfrac{{\sqrt 3 }}{3} \to \varphi = - \dfrac{\pi }{6}\)
=> $u$ chậm pha hơn $i$ một góc $\frac{\pi }{6}$
=> $i$ sớm pha hơn $u$ một góc $\frac{\pi }{6}$
Hướng dẫn giải:
Sử dụng công thức tính \(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}\)