Đề kiểm tra học kì 2 - Đề số 5

Tập nghiệm của bất phương trình $\left| {x - 3} \right| >  - 1$ là

Đường tròn \(\left( C \right)\) đi qua hai điểm \(A\left( { - 1;2} \right),{\rm{ }}B\left( { - 2;3} \right)\) và có tâm \(I\) thuộc đường thẳng \(\Delta :3x - y + 10 = 0.\) Phương trình của đường tròn \(\left( C \right)\) là:

Phương trình nào sau đây là phương trình đường tròn?

Cho biểu thức \(f\left( x \right) = 1 - \dfrac{{2 - x}}{{3x - 2}}.\) Tập hợp tất cả các giá trị của \(x\) thỏa mãn bất phương trình \(f\left( x \right) \le 0\) là

Tập nghiệm của bất phương trình $\left| {{x^2} - 5x + 4} \right| \le {x^2} + 6x + 5$ là:

Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?

Tìm phương trình chính tắc của Elip có tiêu cự bằng $6$ và đi qua điểm $A\left( {0;5} \right)$.

Cho $A,B,C$ là $3$ góc của một tam giác. Hãy xác định hệ thức sai:

Tập nghiệm của bất phương trình \({x^2} - 3x + 2 < 0\) là:

Khẳng định nào sau đây là đúng?

Gọi \(S\) là tập nghiệm của bất phương trình \( - 2 < x < 4\). Chọn mệnh đề đúng:

Cho hàm số \(y = x + \dfrac{1}{{x - 1}}\) xác định trên \(\left( {1; + \infty } \right)\). Gọi $m$ là giá trị nhỏ nhất của hàm số, giá trị của $m$ nằm trong khoảng nào sau đây?

Trong mặt phẳng \(Oxy\), đường thẳng \(\Delta :3x - 2y + 7 = 0\) cắt đường thẳng nào sau đây?

Tìm tập xác định \({\rm{D}}\) của hàm số \(y = \dfrac{{3 - x}}{{\sqrt {4 - 3x - {x^2}} }}.\)

Tập \(S = \left[ { - 1;\dfrac{3}{2}} \right)\) là tập nghiệm của hệ bất phương trình sau đây ?

Chọn đẳng thức sai trong các đẳng thức sau

Cho đường thẳng \(\Delta :\dfrac{{x - 1}}{2} = \dfrac{{y + 3}}{{ - 1}}\) và điểm \(N\left( {1;\, - 4} \right)\). Khoảng cách từ điểm \(N\) đến đường thẳng \(\Delta \) bằng

Cho $\dfrac{\pi }{2} < a < \pi $. Kết quả đúng là

Cho tam giác \(ABC\) với \(A\left( {1;3} \right)\), \(B\left( { - 2;4} \right)\), \(C\left( { - 1;5} \right)\) và đường thẳng \(d:2x - 3y + 6 = 0\). Đường thẳng \(d\) cắt cạnh nào của tam giác \(ABC\)

Cho bốn cung lượng giác (trên một đường tròn định hướng): $\alpha  =  - \dfrac{{5\pi }}{6},$ $\beta  = \dfrac{\pi }{{\rm{3}}}$, $\gamma  = \dfrac{{{\rm{25}}\pi }}{{\rm{3}}},$ $\delta  = \dfrac{{{\rm{19}}\pi }}{{\rm{6}}}$ có cùng điểm đầu. Các cung nào có điểm cuối trùng nhau:

Đơn giản biểu thức \(A = \cos \left( {\alpha  - \dfrac{\pi }{2}} \right) + \sin (\dfrac{\pi }{2} - \alpha ) - \cos \left( {\dfrac{\pi }{2} + \alpha } \right) - \sin \left( {\dfrac{\pi }{2} + \alpha } \right)\) ta được:

Bất phương trình \(ax + b > 0\) có tập nghiệm là \(\mathbb{R}\) khi:

Sản lượng lúa (đơn vị là tạ) của $40$ thửa ruộng thí nghiệm có cùng diện tích được trình bày trong bảng số liệu sau:

Sản lượng trình bình của \(40\) thửa ruộng là:

Công thức nào sau đây đúng về độ lệch chuẩn biết giá trị trung bình \(\overline x \)?

Trên đường tròn lượng giác, khẳng định nào sau đây là đúng?

Cho hai điểm \(A\left( {4;0} \right)\,,\;B\left( {0;5} \right)\). Phương trình nào sau đây không phải là phương trình của đường thẳng $AB$ ?

Tìm tất cả các giá trị của tham số $m$ sao cho tam thức bậc hai $\left( {m - 1} \right){x^2} + \left( {3m - 2} \right)x + 3 - 2m = 0$ đổi dấu hai lần trên \(\mathbb{R}\)?

Bất phương trình ${m^2}\left( {x - 1} \right) \ge 9x + 3m$ nghiệm đúng với mọi \(x\) khi

Tập nghiệm của bất phương trình $2x\left( {4 - x} \right)\left( {3 - x} \right)\left( {3 + x} \right) > 0$ là

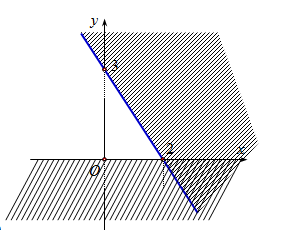
Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D ?

Tập nghiệm của hệ bất phương trình $\left\{ \begin{array}{l}{x^2} - 4x + 3 > 0\\{x^2} - 6x + 8 > 0\end{array} \right.$ là

Xác định $m$ để với mọi \(x\) ta có \( - 1 \le \dfrac{{{x^2} + 5x + m}}{{2{x^2} - 3x + 2}} < 7\).

Cho hai số thực dương \(x,{\rm{ }}y\) thỏa mãn \(x + y + xy \ge 7\). Giá trị nhỏ nhất của \(S = x + 2y\) là:

Tính số đo cung có độ dài của cung bằng $\dfrac{{40}}{3}cm$ trên đường tròn có bán kính $20{\rm{ }}cm$.

Trên đường tròn với điểm gốc là \(A\). Điểm \(M\) thuộc đường tròn sao cho cung lượng giác $AM$ có số đo \({60^0}\). Gọi \(N\) là điểm đối xứng với điểm \(M\) qua trục \(Oy\), số đo cung lượng giác \(AN\) là:

Biểu thức $P = {\cos ^2}x.{\cot ^2}x{\rm{ }} + 3{\cos ^2}x - {\cot ^2}x + 2{\sin ^2}x$ có giá trị là

Biểu thức \(A = \dfrac{{\sin \left( { - {{328}^0}} \right).\sin {{958}^0}}}{{\cot {{572}^0}}} - \dfrac{{\cos \left( { - {{508}^0}} \right).\cos \left( { - {{1022}^0}} \right)}}{{\tan \left( { - {{212}^0}} \right)}}\) rút gọn bằng:

Tính \(A = \cos \dfrac{{2\pi }}{9}\cos \dfrac{{4\pi }}{9}\cos \dfrac{{8\pi }}{9}\)

Trong mặt phẳng tọa độ \(Oxy\), cho điểm \(A\left( {2;\;1} \right)\) và đường thẳng \(\Delta :\left\{ \begin{array}{l}x = - 1 + 2t\\y = 2 + t\end{array} \right.\). Tìm tọa độ điểm \(M\) thuộc đường thẳng \(\Delta \) sao cho \(AM = \sqrt {10} \).

Trong mặt phẳng với hệ tọa độ $Oxy,$ cho $\Delta ABC$ cân có đáy là $BC.$  Đỉnh $A$  có tọa độ là các số dương, hai điểm $B$  và $C$  nằm trên trục $Ox,$  phương trình cạnh $AB:$ $y = 3\sqrt 7 (x - 1)$. Biết chu vi của $\Delta ABC$ bằng $18,$  tìm tọa độ các đỉnh $A,B,C.$

Tìm bán kính \(R\) của đường tròn đi qua ba điểm \(A\left( {0;4} \right)\), \(B\left( {3;4} \right)\), \(C\left( {3;0} \right)\).

Cho đường tròn \((C):{x^2} + {y^2} - 2x + 4y - 4 = 0\). Đường thẳng nào sau đây là tiếp tuyến của đường tròn:

Phương trình chính tắc của elip có một đỉnh là \(B(0; - 2)\), tiêu cự là \(2\sqrt 5 \) là:

Trong mặt phẳng \(\left( {Oxy} \right)\) cho \(\Delta ABC\). Biết phương trình các đường thẳng chứa đường cao \(BH\), phân giác \(AD\) lần lượt là \(3x + 4y + 10 = 0,x - y + 1 = 0\) và điểm \(M\left( {0;2} \right)\) thuộc đường thẳng \(AB\) và \(MC = \sqrt 2 \). Khi đó hoành độ nguyên của điểm \(C\) là

Bất phương trình: $\left| {{x^4} - 2{x^2} - 3} \right| \le {x^2} - 5$ có bao nhiêu nghiệm nghiệm nguyên?

Nếu $\sin \left( {2\alpha  + \beta } \right) = 3\sin \beta ;$ $\cos \alpha  \ne 0;$ $\cos \left( {\alpha  + \beta } \right) \ne 0$ thì $\tan \left( {\alpha  + \beta } \right)$ bằng:

Đơn giản biểu thức \(C = \dfrac{1}{{\sin 10^\circ }} + \dfrac{{\sqrt 3 }}{{\cos 10^\circ }}\).

Tìm giá trị nhỏ nhất của biểu thức $\sin a + \sqrt 3 \cos a$.

Cho phương trình ${x^2} + {y^2} - 2\left( {m + 1} \right)x + 4y - 1 = 0{\rm{   }}\left( 1 \right)$. Với giá trị nào của $m$ để $\left( 1 \right)$ là phương trình đường tròn có bán kính nhỏ nhất?

Tổng các nghiệm nguyên của bất phương trình

\(\sqrt {7x + 7}  + \sqrt {7x - 6}  + 2\sqrt {49{x^2} + 7x - 42}  < 181 - 14x\) là