Kết quả:
0/50
Thời gian làm bài: 00:00:00
Phương trình nào sau đây biểu diễn đường thẳng không song song với đường thẳng \(\left( d \right):\,y = 2x - 1\)?
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
Cho \(\cos \alpha = m\) . Tính \({\sin ^2}\dfrac{\alpha }{2}\)
Khẳng định nào sau đây là đúng khi nói về “đường tròn định hướng”?
Giá trị của biểu thức $S = 3 - {\rm{si}}{{\rm{n}}^2}{\rm{9}}{0^0} + {\rm{ 2co}}{{\rm{s}}^2}{\rm{6}}{{\rm{0}}^0}{\rm{ - 3ta}}{{\rm{n}}^2}{45^0}$ bằng:
Đường tròn tâm $I\left( {a;b} \right)$ và bán kính $R$ có dạng:
Bất phương trình \(2x + \dfrac{3}{{2x - 4}} < 3 + \dfrac{3}{{2x - 4}}\) tương đương với
Cho Elip $\left( E \right)$ có phương trình chính tắc là $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$, với $a > b > 0$. Khi đó khẳng định nào sau đây đúng?
Đường tròn có tâm $I\left( {1;2} \right)$, bán kính $R = 3$ có phương trình là:
Cho biểu thức \(f\left( x \right) = \dfrac{1}{{3x - 6}}.\) Tập hợp tất cả các giá trị của \(x\) để \(f\left( x \right) \le 0\) là
Cho Elip $\left( E \right)$ có phương trình chính tắc là $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$, với $a > b > 0$. Khi đó khẳng định nào sau đây đúng?
Trong mặt phẳng với hệ trục tọa độ \(Oxy\), cho elip \(\left( E \right)\) có độ dài trục lớn bằng 12 và độ dài trục bé bằng 6. Phương trình nào sau đây là phương trình của elip \(\left( E \right)\)
Tìm \(m\) để hệ \(\left\{ \begin{array}{l}{x^2} - 2x + 1 - m \le 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\{x^2} - \left( {2m + 1} \right)x + {m^2} + m \le 0\,\,\,\left( 2 \right)\end{array} \right.\) có nghiệm.
Đường thẳng \(\left( \Delta \right)\): \(3x - 2y - 7 = 0\) cắt đường thẳng nào sau đây?
Trong mặt phẳng với hệ tọa độ $Oxy$ cho hai đường thẳng $\Delta :x + 3y + 8 = 0$, $\Delta ':\,3x - 4y + 10 = 0$ và điểm $A\left( { - 2;1} \right).$ Viết phương trình đường tròn có tâm thuộc đường thẳng \(\Delta \), đi qua điểm $A$ và tiếp xúc với đường thẳng \(\Delta '\)
Đơn giản biểu thức \(A = \cos \left( {\alpha - \dfrac{\pi }{2}} \right) + \sin (\dfrac{\pi }{2} - \alpha ) - \cos \left( {\dfrac{\pi }{2} + \alpha } \right) - \sin \left( {\dfrac{\pi }{2} + \alpha } \right)\) ta được:
Cho đường thẳng \(\left( d \right):2x + 3y - 4 = 0\). Véc tơ nào sau đây là véc tơ chỉ phương của $\left( d \right)$?
Công thức tính giá trị trung bình đối với bảng phân bố tần số rời rạc là:
Đường tròn \(\left( C \right)\) đi qua hai điểm \(A\left( { - 1;2} \right),{\rm{ }}B\left( { - 2;3} \right)\) và có tâm \(I\) thuộc đường thẳng \(\Delta :3x - y + 10 = 0.\) Phương trình của đường tròn \(\left( C \right)\) là:
Với điều kiện nào thì \({x^2} + {y^2} + 2ax + 2by + c = 0,\) biểu diễn phương trình đường tròn.
Trong các khẳng định sau khẳng định nào đúng?
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho tam giác \(ABC\) có $A\left( {1;2} \right),$ $B\left( {0;3} \right)$ và $C\left( {4;0} \right)$. Chiều cao của tam giác kẻ từ đỉnh \(A\) bằng:
Bất phương trình \(\left( {{m^2} + 9} \right)x + 3 \ge m\left( {1 - 6x} \right)\) nghiệm đúng với mọi \(x\) khi
Trên đường tròn lượng giác gốc \(A\) cho các cung có số đo:
\(\left( {\rm{I}} \right)\). \(\dfrac{\pi }{4}\).
\(\left( {{\rm{II}}} \right)\). \( - \dfrac{{7\pi }}{4}\).
\(\left( {{\rm{III}}} \right)\). \(\dfrac{{13\pi }}{4}\).
\(\left( {{\rm{IV}}} \right)\). \( - \dfrac{{5\pi }}{4}\).
Hỏi các cung nào có điểm cuối trùng nhau?
Trong các hình chữ nhật có cùng chu vi thì
Chọn phát biểu đúng:
Mệnh đề nào sau đây sai? Đường thẳng \(\left( d \right)\) được xác định khi biết.
Sản lượng lúa (đơn vị là tạ) của $40$ thửa ruộng thí nghiệm có cùng diện tích được trình bày trong bảng số liệu sau:

Sản lượng trình bình của \(40\) thửa ruộng là:
Giải bất phương trình \( - 2{x^2} + 3x - 7 \ge 0.\)
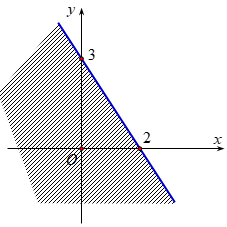
Miền nghiệm (phần không bị gạch) của bất phương trình \(3x - 2y > - 6\) là
Với giá trị nào của $m$ thì bất phương trình ${x^2} - x + m \le 0$ vô nghiệm?
Bất phương trình \(\left( {\left| {x - 1} \right| - 3} \right)\left( {\left| {x + 2} \right| - 5} \right) < 0\) có nghiệm là
Cho góc lượng giác \(\left( {OA,OB} \right)\) có số đo bằng $\dfrac{\pi }{5}$. Hỏi trong các số sau, số nào là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác \(\left( {OA,OB} \right)\)?
Giá trị của biểu thức \(A = \dfrac{{\cos {{750}^0} + \sin {{420}^0}}}{{\sin ( - {{330}^0}) - \cos ( - {{390}^0})}}\). Ta được
Đơn giản biểu thức $A = \left( {1-{{\sin }^2}x} \right).{\cot ^2}x + \left( {1-{{\cot }^2}x} \right),$ ta có
Biết $\cos \left( {\alpha + \beta } \right) = 0$ thì $\sin \left( {\alpha + 2\beta } \right)$ bằng:
Tính giá trị biểu thức \(P = {\left( {\sin a + \sin b} \right)^2} + {\left( {\cos a + \cos b} \right)^2}\) biết \(a - b = \dfrac{\pi }{4}\).
Tam giác vuông cân tại $A$ có $AB = 2a$. Đường trung tuyến $BM$ có độ dài là:
Trong mặt phẳng \(Oxy\), hai đường thẳng \({d_1}:4\,x + 3y - 18 = 0\); \({d_2}:3x + 5y - 19 = 0\) cắt nhau tại điểm có toạ độ
Cho tam giác $ABC$có \(A\left( { - 2;3} \right)\,,B\left( {1; - 2} \right)\,,C\left( { - 5;4} \right).\)Đường trung tuyến $AM$ có phương trình tham số
Cho 4 điểm \(A\left( { - 3;1} \right),B\left( { - 9; - 3} \right),C\left( { - 6;0} \right),D\left( { - 2;4} \right)\). Tìm tọa độ giao điểm của 2 đường thẳng \(AB\) và \(CD\).
Cho tam giác \(ABC\) có diện tích bằng \(S = \dfrac{3}{2}\), hai đỉnh \(A\left( {2;\; - 3} \right)\) và \(B\left( {3;\; - 2} \right)\). Trọng tâm \(G\) nằm trên đường thẳng \(3x - y - 8 = 0\). Tìm tọa độ đỉnh \(C\)?
Tìm giao điểm $2$ đường tròn$\;\left( {{C_1}} \right):{x^2} + {y^2} - 2 = 0$ và $\left( {{C_2}} \right):{x^2} + {y^2} - 2x = 0$
Với những giá trị nào của $m$ thì đường thẳng $\Delta :4x + 3y + m = 0$ tiếp xúc với đường tròn $\left( C \right):{x^2} + {y^2} - 9 = 0$.
Lập phương trình chính tắc của elip $\left( E \right).$ Hình chữ nhật cơ sở của $\left( E \right)$ có một cạnh nằm trên đường thẳng $y - 2 = 0$ và có độ dài đường chéo bằng \(12\).
Để phương trình: $\left| {x + 3} \right|(x - 2) + m - 1 = 0$có đúng một nghiệm, các giá trị của tham số \(m\)là:
Trong mặt phẳng với hệ tọa độ $Oxy,$ cho hình chữ nhật $ABCD$ có điểm $I\left( {6;2} \right)$ là giao điểm của $2$ đường chéo $AC$ và $BD.$ Điểm $M\left( {1;5} \right)$ thuộc đường thẳng $AB$ và trung điểm $E$ của cạnh $CD$ thuộc đường thẳng $\Delta :x + y-5 = 0.$ Viết phương trình đường thẳng $AB.$
Cho tam giác $ABC$ vuông tại $A$ có $AB = 5cm,BC = 13cm$. Gọi góc \(\widehat {ABC} = \alpha \) và \(\widehat {ACB} = \beta \) . Hãy chọn kết luận đúng khi so sánh \(\alpha \) và \(\beta \).
Cho \(a > b > 0\) và \(x = \dfrac{{1 + a}}{{1 + a + {a^2}}}\), \(y = \dfrac{{1 + b}}{{1 + b + {b^2}}}\). Mệnh đề nào sau đây đúng?
Hệ thức nào sai trong bốn hệ thức sau: