Đề kiểm tra học kì 1 - Đề số 7

Cho tam giác \(ABC\), trọng tâm là \(G\). Phát biểu nào là đúng?

Cho tam giác \(ABC\) cân tại \(A\), \(\widehat A = {120^0}\) và \(AB = a\). Tính \(\overrightarrow {BA} .\overrightarrow {CA} \)

Phần không gạch (không kể d) hình sau là miền nghiệm của bất phương trình nào?

Cho hai tập hợp $A{\rm{ }} = \{ 2;{\rm{ }}4;{\rm{ }}6;{\rm{ }}9\} ,{\rm{ }}B{\rm{ }} = \{ 1;{\rm{ }}2;{\rm{ }}3;{\rm{ }}4\} $ . Tập hợp $A{\rm{ }}\backslash {\rm{ }}B$ bằng tập hợp nào sau đây ?

Cho parabol $\left( P \right):{\rm{ }}y = - 3{x^2} + 6x-1$. Khẳng định đúng nhất trong các khẳng định sau là:

Trong các khẳng định sau khẳng định nào đúng?

Cho hình vuông $ABCD$, tính ${\rm{cos}}\left( {\overrightarrow {AB} ,\overrightarrow {CA} } \right)$

Cho $A$  là tập hợp các ước nguyên dương của $6,{\rm{ }}B$ là tập hợp các ước nguyên dương của $12$ . Hãy chọn đáp án đúng ?

Trong các mệnh đề sau, tìm mệnh đề nào sai ?

Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?

Cho \(3\) điểm phân biệt \(A\),\(B\),\(C\). Khi đó khẳng định nào sau đây đúng nhất ?

Chọn phương án trả lời đúng trong các phương án đã cho sau đây.

Mệnh đề "\(\exists x \in \mathbb{R}:{x^2} = 2\)" khẳng định rằng:

Phát biểu nào là sai?

Trong các hàm số sau đây: $y = \left| x \right|$, $y = {x^2} + 4x$, $y = - {x^4} + 2{x^2}$ có bao nhiêu hàm số chẵn?

Cho hình bình hành \(ABCD\) tâm \(O\). Khi đó \(\overrightarrow {OA} + \overrightarrow {BO}  = \)

Trên đường thẳng $MN$ lấy điểm $P$ sao cho \(\overrightarrow {MN} =  - 3\overrightarrow {MP} \). Điểm $P$ được xác định đúng trong hình vẽ nào sau đây:

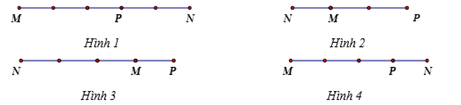
Cho ba vectơ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c $ đều khác vectơ – không. Trong đó hai vectơ $\overrightarrow a ,\overrightarrow b $ cùng hướng, hai vectơ $\overrightarrow a \,,{\rm{ }}\overrightarrow c $ đối nhau. Khẳng định nào sau đây đúng ?

Điểm nào sau đây thuộc đồ thị hàm số $y = 2\left| {x-1} \right| + 3\left| x \right| - 2$?

Giao điểm của parabol \(\left( P \right)\): \(y = {x^2} + 5x + 4\) với trục hoành:

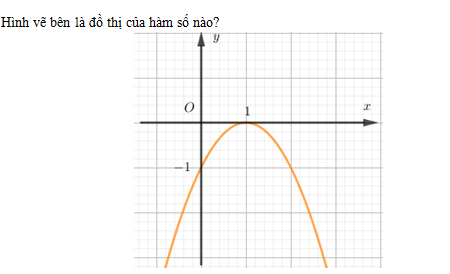
Biết \(\overrightarrow a \), \(\overrightarrow b \)\( \ne \overrightarrow 0 \) và \(\overrightarrow a .\overrightarrow b  =  - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\). Câu nào sau đây đúng

Kí hiệu \(\overline{\overline P} \) là mệnh đề phủ định của \(\overline P \). Khi đó:

Xác định Parabol $\left( P \right):\,\,y = a{x^2} + bx + 3$ biết rằng Parabol có đỉnh $I\left( {3;\,\, - 2} \right)$.

Hai véctơ bằng nhau khi hai véctơ đó có:

Trong tam giác $ABC$, ta có.

Tam giác \(ABC\) có đoạn thẳng nối trung điểm của \(AB\) và \(BC\) bằng \(3\), cạnh \(AB = 9\) và \(\widehat {ACB} = 60^\circ \). Tính độ dài cạnh cạnh \(BC\).

Một mệnh đề có thể có đặc điểm nào sau đây?

Cho biểu thức $P = 3{\sin ^2}x + 4{\cos ^2}x$, biết $\cos x = \dfrac{1}{2}$. Giá trị của \(P\)  bằng:

Cho $A = \left\{ {1;2;3} \right\}$. Trong các khẳng định sau, khẳng định nào sai ?

Xét câu $P\left( n \right)$: “$n$ chia hết cho $12$ ”. Với giá trị nào của $n$ sau đây thì $P\left( n \right)$ là mệnh đề đúng ?

Xác định Parabol $\left( P \right):\,\,y = a{x^2} + bx - 5$ biết rằng Parabol đi qua điểm $A\left( {3;\,\, - 4} \right)$ và có trục đối xứng $x =  - \dfrac{3}{2}$.

Cho mệnh đề \(P \Rightarrow Q\): “Vì \({3^2} + 1\) là số chẵn nên \(3\) là số lẻ”. Chọn mệnh đề đúng:

Cho mệnh đề “\(\forall x \in R,{x^2} + x \ge  - \dfrac{1}{4}\)”. Lập mệnh đề phủ định của mệnh đề $A$ và xét tính đúng sai của nó .

Số các tập con $3$ phần tử có chứa $\alpha ,\pi $ của \(C = \left\{ {\alpha ,\beta ,\xi ,\pi ,\rho ,\eta ,\gamma ,\sigma ,\omega ,\tau } \right\}\) là:

Gọi ${B_n}$  là tập hợp bội số của $n$  trong tập $Z$ các số nguyên. Sự liên hệ giữa $m$  và $n$  sao cho ${B_n} \cap {B_m} = {B_{mn}}$  là:

Cho hệ bất phương trình \(\left\{ \begin{array}{l}2x - \dfrac{3}{2}y \ge 1\\4x - 3y \le 2\end{array} \right.\) có tập nghiệm \(S\). Khẳng định nào sau đây là khẳng định đúng?

Hàm số $y = \dfrac{{x + 1}}{{x - 2m + 1}}$ xác định trên $\left[ {0;1} \right)$ khi:

Tìm giá trị thực của tham số \(m \ne 0\) để hàm số \(y = m{x^2} - 2mx - 3m - 2\) có giá trị nhỏ nhất bằng \( - 10\) trên \(\mathbb{R}.\)

Trong các mệnh đề sau, mệnh đề nào sai:

Cho tam giác $ABC$  có $AB = 8cm,AC = 18cm$ và có diện tích bằng \(64c{m^2}\). Giá trị $\sin \widehat A$  là:

Từ vị trí \(A\) người ta quan sát một cây cao (hình vẽ).

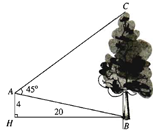
      Biết \(AH = 4{\rm{m}},{\rm{ }}HB = 20{\rm{m}},{\rm{ }}\widehat {BAC} = {45^0}\).

      Chiều cao của cây gần nhất với giá trị nào sau đây?

Cho hình chữ nhật $ABCD$ biết $AB = 4a$ và $AD = 3a$ thì độ dài \(\overrightarrow {AB} + \overrightarrow {AD} \) là:

Cho hai điểm cố định \(A,B\); gọi \(I\) là trung điểm \(AB\). Tập hợp các điểm \(M\) thoả: \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA}  - \overrightarrow {MB} } \right|\) là:

Cho tam giác \(ABC\) có cạnh \(BC = 6\) và đường cao \(AH\left( {H \in BC} \right)\) sao cho \(BH = 2HC\). Tính \(\overrightarrow {AB} .\overrightarrow {BC} \)

Một nhà khoa học đã nghiên cứu về tác động phối hợp của hai loại Vitamin \(A\) và \(B\) đã thu được kết quả như sau: Trong một ngày, mỗi người cần từ 400 đến 1000 đơn vị Vitamin cả \(A\) lẫn \(B\) và có thể tiếp nhận không quá 600 đơn vị vitamin \(A\)và không quá 500 đơn vị vitamin \(B\). Do tác động phối hợp của hai loại vitamin trên nên mỗi ngày một người sử dụng số đơn vị vitamin \(B\) không ít hơn một nửa số đơn vị vitamin \(A\) và không nhiều hơn ba lần số đơn vị vitamin \(A\). Tính số đơn vị vitamin mỗi loại ở trên để một người dùng mỗi ngày sao cho chi phí rẻ nhất, biết rằng mỗi đơn vị vitamin \(A\) có giá 9 đồng và mỗi đơn vị vitamin \(B\) có giá 7,5 đồng.

Muốn đo chiều cao của tháp chàm Por Klong Garai ở Ninh Thuận người ta lấy hai điểm $A$ và $B$ trên mặt đất có khoảng cách $AB = 12\,{\rm{m}}$ cùng thẳng hàng với chân $C$ của tháp để đặt hai giác kế. Chân của giác kế có chiều cao $h = 1,3\,{\rm{m}}$. Gọi $D$ là đỉnh tháp và hai điểm \({A_1}\), \({B_1}\) cùng thẳng hàng với \({C_1}\) thuộc chiều cao $CD$ của tháp. Người ta đo được góc \(\widehat {D{A_1}{C_1}} = 49^\circ \) và \(\widehat {D{B_1}{C_1}} = 35^\circ \). Tính chiều cao $CD$ của tháp.

Gọi M, N lần lượt là trung điểm các cạnh CD, AB của hình bình hành ABCD. Tìm mệnh đề đúng trong các mệnh đề sau:

Cho hai đa thức $f\left( x \right)$ và $g\left( x \right)$ . Xét các tập hợp :

$A = \left\{ {x \in R|f\left( x \right) = 0} \right\};\;B = \left\{ {x \in R|g\left( x \right) = 0} \right\};\;C = \left\{ {x \in R|{f^2}\left( x \right) + {g^2}\left( x \right) = 0} \right\}$

Trong các mệnh đề sau, mệnh đề nào đúng ?

Tìm các giá trị của $m$ để phương trình ${x^2} - 2x + \sqrt {4{x^2} - 12x + 9}  = m$ có nghiệm duy nhất.