Đề kiểm tra học kì 1 - Đề số 8

Với \(\overrightarrow {DE} \) (khác vectơ - không) thì độ dài đoạn \(ED\) được gọi là

Tìm tập xác định của hàm số \(y = \sqrt {x + 5} \).

Cho hình chữ nhật ABCD có AB = a, AC = 2a. Tính góc giữa hai vecto \(\overrightarrow {CA} \) và \(\overrightarrow {DC} .\)

Cho các phát biểu sau, hỏi có bao nhiêu phát biểu là mệnh đề ?

1) Hà Nội là thủ đô của Việt Nam.

2) \(\forall x \in R,\;5x - {x^2} > 1\).

3) $6x + 1 > 3$.

4) Phương trình ${x^2} + 3x-1 = 0$ có nghiệm.

Cho hai mệnh đề \(P\) và \(Q\) là các mệnh đề phủ định của nhau. Chọn mệnh đề đúng:

Trong tam giác \(ABC\) có:

Cho ba vectơ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c $ đều khác vectơ – không. Trong đó hai vectơ $\overrightarrow a ,\overrightarrow b $ cùng hướng, hai vectơ $\overrightarrow a \,,{\rm{ }}\overrightarrow c $ đối nhau. Khẳng định nào sau đây đúng ?

Cho tam giác \(ABC\), trọng tâm là \(G\). Phát biểu nào là đúng?

Trong các khẳng định sau, khẳng định nào sai?

Cho hàm số \(y = a{x^2} + bx + c\left( {a < 0} \right)\) có đồ thị \(\left( P \right)\). Khẳng định nào sau đây là khẳng định đúng?

Cho hình vuông $ABCD$, tính ${\rm{cos}}\left( {\overrightarrow {AB} ,\overrightarrow {CA} } \right)$

Trên đường thẳng $MN$ lấy điểm $P$ sao cho \(\overrightarrow {MN} =  - 3\overrightarrow {MP} \). Điểm $P$ được xác định đúng trong hình vẽ nào sau đây:

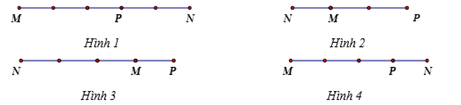
Cho hai hàm số $f\left( x \right)$ và $g\left( x \right)$ cùng đồng biến trên khoảng $\left( {a;b} \right)$. Có thể kết luận gì về chiều biến thiên của hàm số $y = f\left( x \right) + g\left( x \right)$ trên khoảng $\left( {a;b} \right)$?

Cho vectơ $\overrightarrow b \ne \overrightarrow 0 ,{\rm{ }}\overrightarrow a  =  - 2\overrightarrow b {\rm{ }}{\rm{, }}\overrightarrow c  = \overrightarrow a  + \overrightarrow b $. Khẳng định nào sau đây sai?

Tìm mệnh đề đúng

Cho $A$  là tập hợp các ước nguyên dương của $6,{\rm{ }}B$ là tập hợp các ước nguyên dương của $12$ . Hãy chọn đáp án đúng ?

Cho các điểm phân biệt \(A,B,C\). Đẳng thức nào sau đây đúng ?

Cho tập hợp $A = \left\{ {x \in R|\left( {{x^2}-1} \right)\left( {{x^2} + {\rm{ }}2} \right) = 0} \right\}$ . Tập hợp $A$  là:

Đỉnh $I$ của parabol $(P): y = –3x^2+ 6x – 1$ là:

Miền nghiệm của bất phương trình \( - x + 2 + 2\left( {y - 2} \right) < 2\left( {1 - x} \right)\) không chứa điểm:

Cho tập hợp B = \(\left( { - \infty ; - 2} \right] \cap \left[ { - 2; + \infty } \right)\). Khi đó tập hợp $B$ là:

Cho các mệnh đề:

(1) “\(\sqrt 2 \) là số hữu tỉ”.

(2) “\(5\) không chia hết cho \(3\)”.

(3) “Tam giác có tổng số đo các góc bằng \({180^0}\)”.

(4) “Hình vuông có bốn góc bằng nhau”.

Số mệnh đề có mệnh đề phủ định là mệnh đề đúng là:

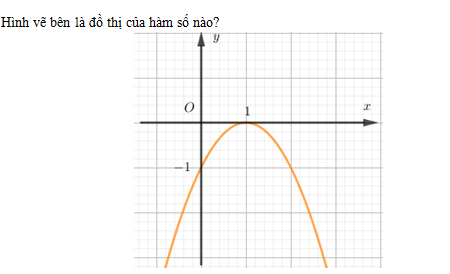
Tìm các giá trị của m để hàm số $y = {x^2} + mx + 5$ luôn đồng biến trên $\left( {1;\,\, + \infty } \right)$.

Cho bất phương trình\( - 2x + \sqrt 3 y + \sqrt 2 \le 0\) có tập nghiệm là \(S\). Khẳng định nào sau đây là khẳng định đúng?

Cho ba điểm $M,N,P$ thẳng hàng, trong đó điểm $N$ nằm giữa hai điểm $M$ và $P$. Khi đó các cặp vecto nào sau đây cùng hướng ?

Cho tam giác $ABC$ có \(\widehat B = {60^0},\widehat C = {45^0}\) và $AB = 5$. Kết quả nào trong các kết quả sau là độ dài của cạnh $AC$?

Tìm giá trị của $m$ để hàm số $y =  - {x^2} + 2x + m - 5$ đạt giá trị lớn nhất bằng $6$

Cho hai tập hợp $X = \left\{ {1;3;5;8} \right\},Y = \left\{ {3;5;7;9} \right\}$ . Tập hợp $X \cup Y$ bằng tập hợp nào sau đây ?

Cho \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ cùng hướng và đều khác vectơ \(\overrightarrow 0 \). Trong các kết quả sau đây, hãy chọn kết quả đúng:

Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

Cho tập $A = \left\{ {1;2;3;4;5;6} \right\}$. Số các tập con khác nhau của $A$ gồm hai phần tử là:

Gọi ${B_n}$  là tập hợp bội số của $n$  trong tập $Z$ các số nguyên. Sự liên hệ giữa $m$  và $n$  sao cho ${B_n} \cap {B_m} = {B_{mn}}$  là:

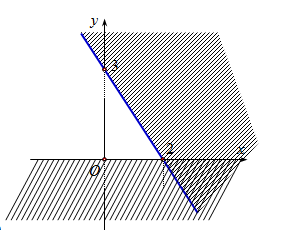
Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D ?

Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc \(\left[ { - 100;100} \right]\) để hàm số \(y = \dfrac{{2x + 2}}{{{x^2} - 3x + 2m - 1}}\) có tập xác định là \(\mathbb{R}?\)

Cho hàm số $y = f(x) = ax^2 + bx +c.$ Rút gọn biểu thức $f(x + 3) – 3f(x + 2) + 3f(x + 1) $ ta được:

Tìm các giá trị của tham số $m$ để $2{x^2} - 2\left( {m + 1} \right)x + {m^2} - 2m + 4 \ge 0 \left( {\forall x} \right)$

Tam giác $ABC$  có $BC = 10$  và \(\widehat A = {30^0}\). Khi đó, bán kính đường tròn ngoại tiếp tam giác $ABC$  là:

Từ vị trí \(A\) người ta quan sát một cây cao (hình vẽ).

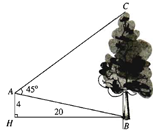
      Biết \(AH = 4{\rm{m}},{\rm{ }}HB = 20{\rm{m}},{\rm{ }}\widehat {BAC} = {45^0}\).

      Chiều cao của cây gần nhất với giá trị nào sau đây?

Cho tam giác $ABC$ với trực tâm $H$. Gọi $D$ là điểm đối xứng với $B$ qua tâm $O$ của đường tròn ngoại tiếp tam giác $ABC$. Khẳng định nào sau đây là đúng ?

Gọi \(G\) là trọng tâm tam giác vuông$ABC$với cạnh huyền $BC = 12$. Tổng hai vectơ $\overrightarrow {GB} + \overrightarrow {GC} $ có độ dài bằng bao nhiêu ?

Cho hình vuông \(ABCD\) cạnh $\;a\sqrt 2 $. Tính$S = \left| {2\overrightarrow {AD} + \overrightarrow {DB} } \right|$?

Cho hình thang vuông \(ABCD\) có đáy lớn \(AB = 4a\), đáy nhỏ \(CD = 2a\), đường cao \(AD = 3a\); \(I\) là trung điểm của \(AD\) . Câu nào sau đây sai?

Gọi M, N lần lượt là trung điểm các cạnh CD, AB của hình bình hành ABCD. Tìm mệnh đề đúng trong các mệnh đề sau:

Tìm các giá trị của tham số m để phương trình $\dfrac{1}{2}{x^2} - 4\left| x \right| + 3 = {m^2}$ có 3 nghiệm thực phân biệt.

Giá trị nhỏ nhất của biết thức $F = y - x$ trên miền xác định bởi hệ $\left\{ {\begin{array}{*{20}{c}}{y - 2x \le 2}\\{2y - x \ge 4}\\{x + y \le 5}\end{array}} \right.$ là.

Cho tam giác $ABC$ vuông tại $A$ có $AB = 5cm,BC = 13cm$. Gọi góc \(\widehat {ABC} = \alpha \) và \(\widehat {ACB} = \beta \) . Hãy chọn kết luận đúng khi so sánh \(\alpha \) và \(\beta \).

Cho $A$  là tập hợp các số tự nhiên chẵn không lớn hơn $10$ .

$B = \{ n \in N/n \le 6\} $  và $C = \{ n \in N/4 \le n \le 10\} $ .

Khi đó ta có câu đúng là: