Đề kiểm tra học kì 1 - Đề số 10

Cho mệnh đề \(P\): “\(35\) là số có hai chữ số”. Mệnh đề \(Q\) nào dưới đây thỏa mãn \(P \Rightarrow {\rm{Q}}\) là mệnh đề sai?

Tìm các giá trị của m để hàm số $y = {x^2} + mx + 5$ luôn đồng biến trên $\left( {1;\,\, + \infty } \right)$.

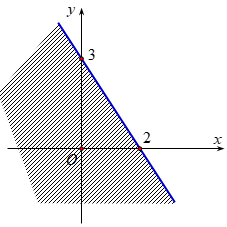
Đẳng thức nào sau đây mô tả đúng hình vẽ bên:

Tam giác $ABC$  có $BC = a,CA = b,AB = c$  và có diện tích $S$ . Nếu tăng cạnh $BC$  lên $2$  lần đồng thời tăng cạnh $CA$  lên $3$  lần và giữ nguyên độ lớn của góc $C$  thì khi đó diện tích tam giác mới được tạo nên bằng:

Cho tập $A = \left[ {-2;4} \right),B = \left( {0;5} \right]$ . Khẳng định nào sau đây sai ?

Tâp hợp \(\left[ {0;4} \right] \cap \left[ {3;5} \right] \) là

Cho biểu thức $P = 3{\sin ^2}x + 4{\cos ^2}x$, biết $\cos x = \dfrac{1}{2}$. Giá trị của \(P\)  bằng:

Cho hai tập hợp: $A = \{ x|x$  là ước số nguyên dương của $12\} $

$B = \{ x|\;x$  là ước số nguyên dương của $18\} $

Tập hợp $A \cap B$ là:

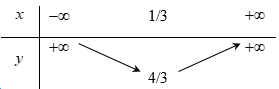
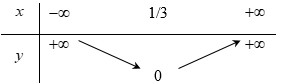
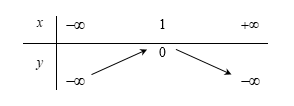
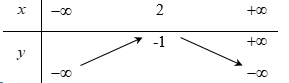
Bảng biến thiên của hàm số $y = –x^2+ 2x – 1$ là:

Cho đồ thị hàm số $y = a{x^2} + bx + c\,$như hình vẽ.

Khẳng định nào sau đây là đúng:

Cho parabol $\left( P \right):{\rm{ }}y = - 3{x^2} + 6x-1$. Khẳng định đúng nhất trong các khẳng định sau là:

Cho hình bình hành $ABCD$. Đẳng thức nào sau đây sai.

Trong các khẳng định sau khẳng định nào đúng?

Kí hiệu \(\overline{\overline P} \) là mệnh đề phủ định của \(\overline P \). Khi đó:

Ký hiệu nào sau đây là để chỉ \(\sqrt 5 \)  không phải là số hữu tỉ ?

Cho tam giác đều $ABC$ cạnh $a$. Khi đó $\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = $

Cho hàm số \(y = a{x^2} + bx + c\left( {a < 0} \right)\) có đồ thị \(\left( P \right)\). Khẳng định nào sau đây là khẳng định đúng?

Miền nghiệm của bất phương trình \( - x + 2 + 2\left( {y - 2} \right) < 2\left( {1 - x} \right)\) không chứa điểm:

Những tính chất nào sau đây chứng tỏ rằng $B$  là một tập con của $A$ ?

Cho \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ cùng hướng và đều khác vectơ \(\overrightarrow 0 \). Trong các kết quả sau đây, hãy chọn kết quả đúng:

Chọn phương án trả lời đúng trong các phương án đã cho sau đây.

Mệnh đề "\(\exists x \in \mathbb{R}:{x^2} = 2\)" khẳng định rằng:

Trong tam giác $ABC$ ta có:

Cho hai tập hợp \(A = \left\{ {1;5} \right\}\) và \(B = \left\{ {1;3;5} \right\}.\) Tìm \(A \cap B.\)

Một mệnh đề có thể có đặc điểm nào sau đây?

Tìm mệnh đề đúng

Phần không gạch (không kể d) hình sau là miền nghiệm của bất phương trình nào?

Cho tam giác $ABC$ với trung tuyến $AM$ và trọng tâm $G$. Khi đó $\overrightarrow {GA} = $

Cho hàm số: $y = f\left( x \right) = \left| {2x - 3} \right|.$ Tìm \(x\) để$f\left( x \right) = 3.$

Cho hình vuông $ABCD$, khẳng định nào sau đây đúng:

Xác định Parabol $\left( P \right):\,\,y = a{x^2} + bx - 5$ biết rằng Parabol đi qua điểm $A\left( {3;\,\, - 4} \right)$ và có trục đối xứng $x =  - \dfrac{3}{2}$.

Tập xác định của hàm số $y = \dfrac{{x - 1}}{{{x^2} - x + 3}}$ là

Cho hình chữ nhật ABCD có AB = a, AC = 2a. Tính góc giữa hai vecto \(\overrightarrow {CA} \) và \(\overrightarrow {DC} .\)

Cho các điểm phân biệt \(A,B,C\). Đẳng thức nào sau đây đúng ?

Trên một tấm bìa cac-tông có ghi 4 mệnh đề sau:

     I. Trên tấm bìa này có đúng một mệnh đề sai.

     II. Trên tấm bìa này có đúng hai mệnh đề sai.

     III. Trên tấm bìa này có đúng ba mệnh đề sai.

     IV. Trên tấm bìa này có đúng bốn mệnh đề sai.

Hỏi trên tấm bìa trên có bao nhiêu mệnh đề sai?

Xác định tính đúng sai của mệnh đề sau và tìm phủ định của nó :

F: " \(\exists  a \in \mathbb{R}\):  \(a + 1 + \dfrac{1}{{a + 1}} \le 2\)"

Cho tập  hợp $A = \{ x \in N|x$ là ước chung của $36$ và $120\} $. Các phần tử của tập $A$ là:

Miền nghiệm (phần không bị gạch) của bất phương trình \(3x - 2y >  - 6\) là

Cho hệ bất phương trình \(\left\{ \begin{array}{l}2x - \dfrac{3}{2}y \ge 1\\4x - 3y \le 2\end{array} \right.\) có tập nghiệm \(S\). Khẳng định nào sau đây là khẳng định đúng?

Hàm số $y = \dfrac{{x + 1}}{{x - 2m + 1}}$ xác định trên $\left[ {0;1} \right)$ khi:

Viết phương trình của Parabol $(P)$ biết rằng $(P)$ đi qua các điểm $A\left( {0;\,\,2} \right),\,\,B\left( { - 2;\,\,5} \right),\,\,C\left( {3;\,\,8} \right)$

Rút gọn biểu thức ${\rm{S}} = \cos {\rm{(9}}{{\rm{0}}^0} - x)\sin \left( {{{180}^0} - x} \right) $ $- {\rm{\sin (9}}{{\rm{0}}^0} - x)\cos \left( {{{180}^0} - x} \right)$ ta được kết quả:

Cho góc \(\widehat {xOy} = 30^\circ \). Gọi \(A\) và \(B\) là hai điểm di động lần lượt trên \(Ox\) và \(Oy\) sao cho \(AB = 1\). Độ dài lớn nhất của đoạn \(OB\) bằng:

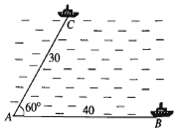
Hai chiếc tàu thủy cùng xuất phát từ một vị trí \(A\), đi thẳng theo hai hướng tạo với nhau góc \({60^0}\). Tàu \(B\) chạy với tốc độ \(20\) hải lí một giờ. Tàu \(C\) chạy với tốc độ \(15\) hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí? Kết quả gần nhất với số nào sau đây?

Cho lục giác đều $ABCDEF$ và $O$ là tâm của nó. Đẳng thức nào dưới đây là đẳng thức sai?

Cho hai điểm cố định \(A,B\); gọi \(I\) là trung điểm \(AB\). Tập hợp các điểm \(M\) thoả: \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA}  - \overrightarrow {MB} } \right|\) là:

Đề mẫu ĐGNL 2019

Một bác nông dân cần trồng lúa và khoai trên diện tích đất gồm 6 ha, với lượng phân bón dữ trữ là 100kg và sử dụng tối đa 120 ngày công. Để trồng 1 ha lúa cần sử dụng 20kg phân bón, 10 ngày công với lợi nhuận là 30 triệu đồng, để trồng 1 ha khoai cần sử dụng 10 kg phân bón, 30 ngày công với lợi nhuận là 60 triệu đồng. Để đạt được lợi nhuận cao nhất, bác nông dân đã trồng \(x\left( {ha} \right)\) lúa và \(y\left( {ha} \right)\) khoai. Giá trị của \(x\) là:

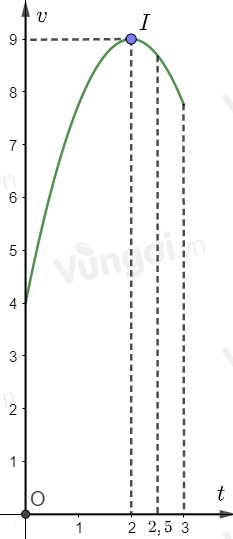
Một vật chuyển động trong 3 giờ với vận tốc  \(v\,\,\left( {km/h} \right)\) phụ thuộc thời gian \(t\,\,\left( h \right)\)  có đồ thị là một phần của parabol có đỉnh \(I\left( {2;\,\,9} \right)\) và trục đối xứng song song với trục tung như hình vẽ. Vận tốc của vật tại thời điểm 2 giờ 30 phút sau khi vật bắt đầu chuyển động gần bằng giá trị nào nhất trong các giá trị sau?

Muốn đo chiều cao của tháp chàm Por Klong Garai ở Ninh Thuận người ta lấy hai điểm $A$ và $B$ trên mặt đất có khoảng cách $AB = 12\,{\rm{m}}$ cùng thẳng hàng với chân $C$ của tháp để đặt hai giác kế. Chân của giác kế có chiều cao $h = 1,3\,{\rm{m}}$. Gọi $D$ là đỉnh tháp và hai điểm \({A_1}\), \({B_1}\) cùng thẳng hàng với \({C_1}\) thuộc chiều cao $CD$ của tháp. Người ta đo được góc \(\widehat {D{A_1}{C_1}} = 49^\circ \) và \(\widehat {D{B_1}{C_1}} = 35^\circ \). Tính chiều cao $CD$ của tháp.

Cho hai đa thức $f\left( x \right)$ và $g\left( x \right)$ . Xét các tập hợp :

\(\begin{array}{l}A = \left\{ {x \in R|f\left( x \right) = 0} \right\}\\B = \left\{ {x \in R|g\left( x \right) = 0} \right\}\\C = \left\{ {x \in R|\dfrac{{f\left( x \right)}}{{g\left( x \right)}} = 0} \right\}\end{array}\)

Trong các mệnh đề sau, mệnh đề nào đúng ?

Gọi M, N lần lượt là trung điểm các cạnh CD, AB của hình bình hành ABCD. Tìm mệnh đề đúng trong các mệnh đề sau: