Đề kiểm tra giữa học kì 1- Đề số 3

Cho hai tập hợp $A = \{ 0;1;2;3;4\} ,B = \{ 1;2;3\} $ . Trong các mệnh đề sau, tìm mệnh đề sai ?

Cho bất phương trình\( - 2x + \sqrt 3 y + \sqrt 2 \le 0\) có tập nghiệm là \(S\). Khẳng định nào sau đây là khẳng định đúng?

Cho bất phương trình bậc nhất hai ẩn \(x + 2y \ge 0\).

Với y=0, có bao nhiêu giá trị của x thỏa mãn bất phương trình đã cho?

Cho tập hợp $A = \left\{ {x \in R|\left( {{x^2}-1} \right)\left( {{x^2} + {\rm{ }}2} \right) = 0} \right\}$ . Tập hợp $A$  là:

Trong các mệnh đề sau, mệnh đề sai là:

Phần không gạch (không kể d) hình sau là miền nghiệm của bất phương trình nào?

Cho $A = \left\{ {1;2;3} \right\}$. Trong các khẳng định sau, khẳng định nào sai ?

Tam giác $ABC$  có ba cạnh là $5,12,13$. Khi đó, diện tích tam giác là:

Chọn phương án trả lời đúng trong các phương án đã cho sau đây.

Mệnh đề "\(\exists x \in \mathbb{R}:{x^2} = 2\)" khẳng định rằng:

Cho các phát biểu sau, hỏi có bao nhiêu phát biểu là mệnh đề ?

1) Hà Nội là thủ đô của Việt Nam.

2) \(\forall x \in R,\;5x - {x^2} > 1\).

3) $6x + 1 > 3$.

4) Phương trình ${x^2} + 3x-1 = 0$ có nghiệm.

Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình$\left\{ {\begin{array}{*{20}{c}}{2x + 3y - 1 > 0}\\{5x - y + 4 < 0}\end{array}} \right.$?

Trong các mệnh đề sau đây, mệnh đề nào đúng?

Những tính chất nào sau đây chứng tỏ rằng $B$  là một tập con của $A$ ?

Mệnh đề \(P \Leftrightarrow Q\) chỉ đúng khi nào?

Các phương án sau, đâu là một mệnh đề đúng?

Ký hiệu nào sau đây là để chỉ \(\sqrt 5 \)  không phải là số hữu tỉ ?

Cho hai tập hợp $X = \left\{ {1;3;5;8} \right\},Y = \left\{ {3;5;7;9} \right\}$ . Tập hợp $X \cup Y$ bằng tập hợp nào sau đây ?

Miền nghiệm của bất phương trình \( - x + 2 + 2\left( {y - 2} \right) < 2\left( {1 - x} \right)\) không chứa điểm:

Trong tam giác $ABC$, ta có.

Trong các khẳng định sau khẳng định nào đúng?

Cho tam giác $ABC$  có $b = 10,c = 16$  và góc \(\widehat A = {60^0}\). Kết quả nào trong các kết quả sau là độ dài của cạnh $BC$?

Để tính $cos{120^0}$ , một học sinh làm như sau:

$(I)\sin {120^0} = \dfrac{{\sqrt 3 }}{2} \Rightarrow (II){\cos ^2}{120^0} = 1 - {\sin ^2}{120^0} \Rightarrow (III){\cos ^2}{120^0} = \dfrac{1}{4} \Rightarrow (IV)\cos {120^0} = \dfrac{1}{2}$

Lập luận trên sai từ bước nào?

Trong tam giác $ABC$, tìm hệ thức sai.

Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?

Trong các mệnh đề sau, tìm mệnh đề nào sai ?

Trong tam giác $ABC$ ta có:

Mệnh đề đảo của mệnh đề “Ba số tự nhiên liên tiếp thì có tổng chia hết cho \(3\)” được phát biểu là:

Cho tập $A \ne \emptyset $ . Trong các mệnh đề sau, tìm mệnh đề sai ?

Cho $A$  là tập hợp các ước nguyên dương của $6,{\rm{ }}B$ là tập hợp các ước nguyên dương của $12$ . Hãy chọn đáp án đúng ?

Phủ định của mệnh đề “\(9\) không phải số nguyên tố” là:

Trên một tấm bìa cac-tông có ghi 4 mệnh đề sau:

     I. Trên tấm bìa này có đúng một mệnh đề sai.

     II. Trên tấm bìa này có đúng hai mệnh đề sai.

     III. Trên tấm bìa này có đúng ba mệnh đề sai.

     IV. Trên tấm bìa này có đúng bốn mệnh đề sai.

Hỏi trên tấm bìa trên có bao nhiêu mệnh đề sai?

Cho các mệnh đề:

(1) “\(\sqrt 3 \) là số vô tỉ nếu và chỉ nếu \(3\) là số hữu tỉ”.

(2) “Tứ giác là hình bình hành nếu và chỉ nếu nó là hình thang có hai cạnh bên bằng nhau”.

(3) “Tứ giác là hình thoi nếu và chỉ nếu nó là hình bình hành có hai cạnh kề bằng nhau ”.

(4) “\(3 > 4\) khi và chỉ khi \(1 > 2\)”.

Số mệnh đề sai là:

Cho mệnh đề “\(\forall x \in R,{x^2} + x \ge  - \dfrac{1}{4}\)”. Lập mệnh đề phủ định của mệnh đề $A$ và xét tính đúng sai của nó .

Xác định tính đúng sai của mệnh đề sau và tìm phủ định của nó :

F: " \(\exists  a \in \mathbb{R}\):  \(a + 1 + \dfrac{1}{{a + 1}} \le 2\)"

Tìm $m$ để \(\left( { - \infty ;1} \right] \cap \left( {m;m + 1} \right) = \emptyset \)

Lớp 10B₁ có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 3 học sinh giỏi cả  Toán và Lý, 4 học sinh giỏi cả Toán và Hóa, 2 học sinh giỏi cả Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10B₁ là:

Ông An muốn thuê một chiếc ô tô (có lái xe) trong một tuần. Giá thuê xe được cho như bảng sau:

Giả sử, từ thứ Hai đến thứ Sáu, tổng số kilômét ông An đi là x (km) và trong hai ngày cuối tuần, tổng số kilômét ông An đi là y (km). Viết bất phương trình biểu thị mối liên hệ giữa x và y sao cho

tổng số tiền ông An phải trả không quá 14 triệu đồng.

Miền biểu diễn nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}y \ge  - 2\\x \ge 2\\2x + y \le 8\end{array} \right.\) có diện tích bằng bao nhiêu?

Cho $A = \cos {235^0}.\sin {60^0}.\tan {125^0}.\cos {90^0}{\rm{ }}$. Khẳng định nào sau đây đúng?

Tam giác vuông cân tại $A$  có $AB = 2a$. Đường trung tuyến $BM$ có độ dài là:

Cho tam giác $ABC$  có $AB = 8cm,AC = 18cm$ và có diện tích bằng \(64c{m^2}\). Giá trị $\sin \widehat A$  là:

Từ vị trí \(A\) người ta quan sát một cây cao (hình vẽ).

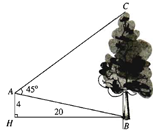
      Biết \(AH = 4{\rm{m}},{\rm{ }}HB = 20{\rm{m}},{\rm{ }}\widehat {BAC} = {45^0}\).

      Chiều cao của cây gần nhất với giá trị nào sau đây?

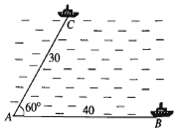
Hai chiếc tàu thủy cùng xuất phát từ một vị trí \(A\), đi thẳng theo hai hướng tạo với nhau góc \({60^0}\). Tàu \(B\) chạy với tốc độ \(20\) hải lí một giờ. Tàu \(C\) chạy với tốc độ \(15\) hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí? Kết quả gần nhất với số nào sau đây?

Một công ty kinh chuẩn bị cho đợt khuyến mại nhằm mục đích thu hút khác hàng bằng cách tiến hành quảng cáo sản phẩm của công ty trên internet và truyền hình. Chi phí cho 1 phút quảng cáo trên internet là 800.000 đồng, trên sóng truyền hình là 4.000.000 đồng. Trang internet chỉ nhận phát các chương trình quảng cáo ngắn nhất là 5 phút. Do nhu cầu quảng cáo trên truyền hình lớn nên đài truyền hình chỉ nhận phát các chương trình dì tối đa là 4 phút. Theo các phân tích, cùng thời lượng một phút quảng cáo, trên truyền hình sẽ có hiệu quả gấp 6 lần trên internet. Công ty dự định chi tối đa 16.000.000 đồng cho quảng cáo. Công ty cần đặt thời lượng quảng cáo trên internet và truyền hình như thế nào để hiệu quả nhất?

Cho hai đa thức $f\left( x \right)$ và $g\left( x \right)$ . Xét các tập hợp :

\(\begin{array}{l}A = \left\{ {x \in R|f\left( x \right) = 0} \right\}\\B = \left\{ {x \in R|g\left( x \right) = 0} \right\}\\C = \left\{ {x \in R|\dfrac{{f\left( x \right)}}{{g\left( x \right)}} = 0} \right\}\end{array}\)

Trong các mệnh đề sau, mệnh đề nào đúng ?

Cho tam giác $ABC$ có $a = 5$ ${\rm{cm}}$, $c = 9$ ${\rm{cm}}$, $\cos C =  - \dfrac{1}{{10}}$. Tính độ dài đường cao ${h_a}$ hạ từ $A$ của tam giác $ABC$.

Giá trị của $a$  mà \(\left[ {a;\dfrac{{a + 1}}{2}} \right] \subset \left(( - \infty ; - 1) \cup (1; + \infty )\right)\) là

Giá trị lớn nhất của $6{\cos ^2}x + 6\sin x-2$  là: