Đề kiểm tra học kì 1 - Đề số 6

Tìm các giá trị của m để hàm số $y = {x^2} + mx + 5$ luôn đồng biến trên $\left( {1;\,\, + \infty } \right)$.

Những tính chất nào sau đây chứng tỏ rằng $B$  là một tập con của $A$ ?

Chọn phương án trả lời đúng trong các phương án đã cho sau đây.

Mệnh đề "\(\exists x \in \mathbb{R}:{x^2} = 2\)" khẳng định rằng:

Trong các khẳng định sau khẳng định nào đúng?

Hình vẽ sau đây (phần không bị gạch) minh họa cho một tập con của tập số thực. Hỏi tập đó là tập nào ?

Giá trị của biểu thức $P = m\sin {0^0} + {\rm{ ncos}}{{\rm{0}}^0}{\rm{  +  p}}\sin {90^0}$ bằng:

Mệnh đề đảo của mệnh đề “Ba số tự nhiên liên tiếp thì có tổng chia hết cho \(3\)” được phát biểu là:

Câu nào sau đây đúng?

Tìm mệnh đề đúng

Cho mệnh đề : “Nếu một tứ giác là hình thang cân thì tứ giác đó có hai đường chéo bằng nhau”. Mệnh đề nào sau đây tương đương với mệnh đề đã cho ?

Cho tam giác $ABC$ có \(\widehat B = {60^0},\widehat C = {45^0}\) và $AB = 5$. Kết quả nào trong các kết quả sau là độ dài của cạnh $AC$?

Cho hình chữ nhật ABCD có AB = a, AC = 2a. Tính góc giữa hai vecto \(\overrightarrow {CA} \) và \(\overrightarrow {DC} .\)

Xác định Parabol $\left( P \right):\,\,y = a{x^2} + bx + 3$ biết rằng Parabol có đỉnh $I\left( {3;\,\, - 2} \right)$.

Phần không gạch (không kể d) hình sau là miền nghiệm của bất phương trình nào?

Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình$\left\{ {\begin{array}{*{20}{c}}{2x + 3y - 1 > 0}\\{5x - y + 4 < 0}\end{array}} \right.$?

Trên đường thẳng $MN$ lấy điểm $P$ sao cho \(\overrightarrow {MN} =  - 3\overrightarrow {MP} \). Điểm $P$ được xác định đúng trong hình vẽ nào sau đây:

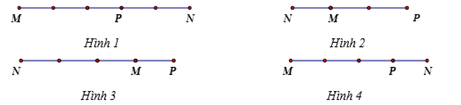
Cho tam giác \(ABC\), trọng tâm là \(G\). Phát biểu nào là đúng?

Cho hình vuông $ABCD$, tính ${\rm{cos}}\left( {\overrightarrow {AB} ,\overrightarrow {CA} } \right)$

Tập xác định của hàm số $y = \left\{ \begin{array}{l}\sqrt {3 - x} ,x \in \left( { - \infty ;0} \right)\\\sqrt {\dfrac{1}{x}} ,x \in \left( {0; + \infty } \right)\end{array} \right.$ là:

Cho hai tập hợp: $A = \{ x|x$  là ước số nguyên dương của $12\} $

$B = \{ x|\;x$  là ước số nguyên dương của $18\} $

Tập hợp $A \cap B$ là:

Cho vectơ $\overrightarrow b \ne \overrightarrow 0 ,{\rm{ }}\overrightarrow a  =  - 2\overrightarrow b {\rm{ }}{\rm{, }}\overrightarrow c  = \overrightarrow a  + \overrightarrow b $. Khẳng định nào sau đây sai?

Cho \(3\) điểm phân biệt \(A\),\(B\),\(C\). Khi đó khẳng định nào sau đây đúng nhất ?

Cho hai mệnh đề \(P,Q\). Phủ định của mệnh đề \(Q\) là:

Biết parabol $(P): y = ax^2+ 2x + 5$ đi qua điểm $A(2; 1).$ Giá trị của $a$ là:

Trong tam giác $ABC$ ta có:

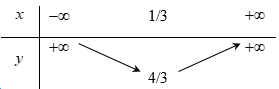
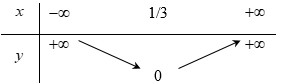
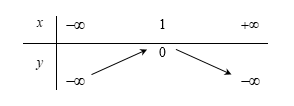
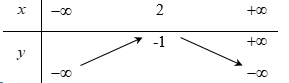
Bảng biến thiên của hàm số $y = –x^2+ 2x – 1$ là:

Giao điểm của parabol \(\left( P \right)\): \(y = {x^2} + 5x + 4\) với trục hoành:

Cho bất phương trình bậc nhất hai ẩn \(x + 2y \ge 0\).

Với y=0, có bao nhiêu giá trị của x thỏa mãn bất phương trình đã cho?

Cho hai tập \(A = \{ x \in R\left| {x + 3 < 4 + 2x\} } \right.\) và \(B = \{ x \in R\left| {5x - 3 < 4x - 1\} } \right.\)

Tất cả các số tự nhiên thuộc cả hai tập $A$  và $B$  là:

Véctơ là một đoạn thẳng

Cho 3 điểm$A,{\rm{ }}B,{\rm{ }}C$. Đẳng thức nào sau đây đúng.

Cho tập hợp B = \(\left( { - \infty ; - 2} \right] \cap \left[ { - 2; + \infty } \right)\). Khi đó tập hợp $B$ là:

Cho mệnh đề \(P \Rightarrow Q\): “Vì \({3^2} + 1\) là số chẵn nên \(3\) là số lẻ”. Chọn mệnh đề đúng:

Cho mệnh đề “\(\forall x \in R,{x^2} + x \ge  - \dfrac{1}{4}\)”. Lập mệnh đề phủ định của mệnh đề $A$ và xét tính đúng sai của nó .

Số các tập con $3$ phần tử có chứa $\alpha ,\pi $ của \(C = \left\{ {\alpha ,\beta ,\xi ,\pi ,\rho ,\eta ,\gamma ,\sigma ,\omega ,\tau } \right\}\) là:

Gọi ${B_n}$  là tập hợp bội số của $n$  trong $N$ . Tập hợp ${B_3} \cap {B_6}$ là:

Ông An muốn thuê một chiếc ô tô (có lái xe) trong một tuần. Giá thuê xe được cho như bảng sau:

Giả sử, từ thứ Hai đến thứ Sáu, tổng số kilômét ông An đi là x (km) và trong hai ngày cuối tuần, tổng số kilômét ông An đi là y (km). Viết bất phương trình biểu thị mối liên hệ giữa x và y sao cho

tổng số tiền ông An phải trả không quá 14 triệu đồng.

Cho hệ bất phương trình \(\left\{ \begin{array}{l}2x - \dfrac{3}{2}y \ge 1\\4x - 3y \le 2\end{array} \right.\) có tập nghiệm \(S\). Khẳng định nào sau đây là khẳng định đúng?

Hàm số $y = \sqrt {\dfrac{{{x^3}}}{{\left| x \right| - 2}}} $ có tập xác định là:

Biết đồ thị hàm số $\left( P \right):\,\,y = {x^2} - \left( {{m^2} + 1} \right)x - 1$ cắt trục hoành tại hai điểm phân biệt có hoành độ \({x_1},{x_2}.\) Tìm giá trị của tham số $m$  để biểu thức $T = {x_1} + {x_2}$ đạt giá trị nhỏ nhất.

Cho tam giác $ABC$ và các mệnh đề

\((I){\rm{  }}\cos \dfrac{{B + C}}{2} = \sin \dfrac{A}{2}\)

\((II){\rm{  }}\tan \dfrac{{A + B}}{2}.\tan \dfrac{C}{2} = 1\)

\((III){\rm{  }}\cos (A + B - C) = \cos 2C\)

Mệnh đề nào đúng?

Cho góc \(\widehat {xOy} = 30^\circ \). Gọi \(A\) và \(B\) là hai điểm di động lần lượt trên \(Ox\) và \(Oy\) sao cho \(AB = 1\). Độ dài lớn nhất của đoạn \(OB\) bằng:

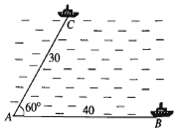
Hai chiếc tàu thủy cùng xuất phát từ một vị trí \(A\), đi thẳng theo hai hướng tạo với nhau góc \({60^0}\). Tàu \(B\) chạy với tốc độ \(20\) hải lí một giờ. Tàu \(C\) chạy với tốc độ \(15\) hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí? Kết quả gần nhất với số nào sau đây?

Cho \(\Delta ABC\) vuông tại \(A\) và \(AB = 3\), \(AC = 4\). Véctơ \(\overrightarrow {CB} + \overrightarrow {AB} \) có độ dài bằng

Cho ba điểm \(A,B,C\) phân biệt. Tập hợp những điểm \(M\) mà \(\overrightarrow {CM} .\overrightarrow {CB}  = \overrightarrow {CA} .\overrightarrow {CB} \) là:

Tìm giá trị nhỏ nhất của biểu thức $P = 3\left( {\dfrac{{{a^2}}}{{{b^2}}} + \dfrac{{{b^2}}}{{{a^2}}}} \right) - 8\left( {\dfrac{a}{b} + \dfrac{b}{a}} \right)$.

Giá trị của $a$  mà \(\left[ {a;\dfrac{{a + 1}}{2}} \right] \subset \left(( - \infty ; - 1) \cup (1; + \infty )\right)\) là

Cho tam giác đều \(ABC\) cạnh \(a.\) Biết rằng tập hợp các điểm \(M\) thỏa mãn đẳng thức \(\left| {2\overrightarrow {MA}  + 3\overrightarrow {MB}  + 4\overrightarrow {MC} } \right| = \left| {\overrightarrow {MB}  - \overrightarrow {MA} } \right|\) là đường tròn cố định có bán kính \(R.\) Tính bán kính \(R\) theo \(a.\)

Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa $24$ $g$ hương liệu, $9$ lít nước và $210$ $g$ đường để pha chế nước cam và nước táo.

+ Để pha chế $1$ lít nước cam cần $30$ $g$ đường, $1$ lít nước và $1$ $g$ hương liệu;

+ Để pha chế $1$ lít nước táo cần $10$ $g$ đường, $1$ lít nước và $4$ $g$ hương liệu.

Mỗi lít nước cam nhận được $60$ điểm thưởng, mỗi lít nước táo nhận được $80$ điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?

Cho tam giác $ABC$ có $a = 5$ ${\rm{cm}}$, $c = 9$ ${\rm{cm}}$, $\cos C =  - \dfrac{1}{{10}}$. Tính độ dài đường cao ${h_a}$ hạ từ $A$ của tam giác $ABC$.