Trả lời bởi giáo viên
Đáp án đúng: a
Hàm số y=√x3|x|−2 xác định nếu x3|x|−2≥0.
Ta có: |x|−2=0⇔[x=2x=−2;x3=0⇔x=0
Xét dấu biểu thức x3|x|−2 ta có:
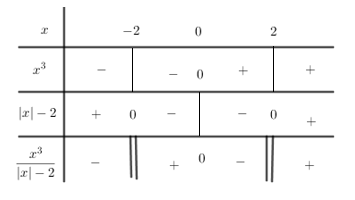
Khi đó tập xác định của hàm số là (−2;0]∪(2;+∞).
Hướng dẫn giải:
- Hàm số phân thức f(x)=1P(x) xác định nếu P(x)≠0.
- Hàm số căn thức √P(x) xác định nếu P(x)≥0.
- Hàm số √1P(x) xác định nếu P(x)>0.
Giải thích thêm:
Một số em có thể sẽ chọn nhầm đáp án D vì tìm thiếu nghiệm x=−2 khi xét dấu.


