Đề kiểm tra học kì 1 - Đề số 7

Sử dụng ký hiệu khoảng để viết tập hợp sau đây: $E = \left( {4; + \infty } \right)\backslash \left( {-\infty ;2} \right]$.

Cho hai tập hợp $A{\rm{ }} = \{ 2;{\rm{ }}4;{\rm{ }}6;{\rm{ }}9\} ,{\rm{ }}B{\rm{ }} = \{ 1;{\rm{ }}2;{\rm{ }}3;{\rm{ }}4\} $ . Tập hợp $A{\rm{ }}\backslash {\rm{ }}B$ bằng tập hợp nào sau đây ?

Cho hình bình hành $ABCD$. Đẳng thức nào sau đây sai.

Mệnh đề nào sau đây đúng ?

Cho hai mệnh đề \(P,Q\), chọn mệnh đề đúng:

Trong các khẳng định sau, khẳng định nào sai?

Cho $\overrightarrow a = \left( {x;2} \right),\overrightarrow b  = \left( { - 5;1} \right),\overrightarrow c  = \left( {x;7} \right)$. Vec tơ $\overrightarrow c  = 2\overrightarrow a  + 3\overrightarrow b $ nếu:

Trong mặt phẳng \(Oxy\) cho \(\overrightarrow a = \left( {1;3} \right),\;\overrightarrow b  = \left( { - 2;1} \right)\). Tích vô hướng của 2 vectơ \(\overrightarrow a .\overrightarrow b \) là:

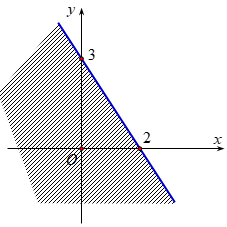
Cho bất phương trình bậc nhất hai ẩn \(x + 2y \ge 0\).

Với y=0, có bao nhiêu giá trị của x thỏa mãn bất phương trình đã cho?

Trên đường thẳng $MN$ lấy điểm $P$ sao cho \(\overrightarrow {MN} =  - 3\overrightarrow {MP} \). Điểm $P$ được xác định đúng trong hình vẽ nào sau đây:

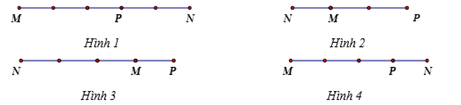
Cho tam giác \(ABC\), trọng tâm là \(G\). Phát biểu nào là đúng?

Các phát biểu nào sau đây không thể là phát biểu của mệnh đề đúng \(P \Rightarrow Q\)

Tam giác $ABC$  có $BC = a,CA = b,AB = c$  và có diện tích $S$ . Nếu tăng cạnh $BC$  lên $2$  lần đồng thời tăng cạnh $CA$  lên $3$  lần và giữ nguyên độ lớn của góc $C$  thì khi đó diện tích tam giác mới được tạo nên bằng:

Phát biểu nào là sai?

Tập \(A = \{ x \in R\left| {1 < x \le 2\} } \right.\) được viết lại dưới dạng đoạn, khoảng là:

Cho vectơ $\overrightarrow b \ne \overrightarrow 0 ,{\rm{ }}\overrightarrow a  =  - 2\overrightarrow b {\rm{ }}{\rm{, }}\overrightarrow c  = \overrightarrow a  + \overrightarrow b $. Khẳng định nào sau đây sai?

Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình$\left\{ {\begin{array}{*{20}{c}}{2x + 3y - 1 > 0}\\{5x - y + 4 < 0}\end{array}} \right.$?

Cho tam giác đều \(ABC\) cạnh \(a = 2\). Hỏi mệnh đề nào sau đây sai?

Trong tam giác $ABC$, tìm hệ thức sai.

Cho hai tập \(A = \{ x \in R\left| {x + 3 < 4 + 2x\} } \right.\) và \(B = \{ x \in R\left| {5x - 3 < 4x - 1\} } \right.\)

Tất cả các số tự nhiên thuộc cả hai tập $A$  và $B$  là:

Để tính $cos{120^0}$ , một học sinh làm như sau:

$(I)\sin {120^0} = \dfrac{{\sqrt 3 }}{2} \Rightarrow (II){\cos ^2}{120^0} = 1 - {\sin ^2}{120^0} \Rightarrow (III){\cos ^2}{120^0} = \dfrac{1}{4} \Rightarrow (IV)\cos {120^0} = \dfrac{1}{2}$

Lập luận trên sai từ bước nào?

Cho \(\overrightarrow a = (0,1)\),\(\overrightarrow b  = ( - 1;2)\),\(\overrightarrow c  = ( - 3; - 2)\). Tọa độ của \(\overrightarrow u  = 3\overrightarrow a  + 2\overrightarrow b  - 4\overrightarrow c \)

Mệnh đề nào sau đây sai?

Cho các phát biểu sau, hỏi có bao nhiêu phát biểu là mệnh đề ?

1) Hà Nội là thủ đô của Việt Nam.

2) \(\forall x \in R,\;5x - {x^2} > 1\).

3) $6x + 1 > 3$.

4) Phương trình ${x^2} + 3x-1 = 0$ có nghiệm.

Cho các điểm phân biệt \(A,B,C\). Đẳng thức nào sau đây đúng ?

Trong tam giác $ABC$ ta có:

Cho bất phương trình \(2x + 3y - 6 \le 0\,\,(1)\). Chọn khẳng định đúng trong các khẳng định sau

Cho \(M\) là trung điểm \(AB\), tìm biểu thức sai:

Cho các vectơ \(\overrightarrow a = \left( {1; - 2} \right),\,\,\overrightarrow b  = \left( { - 2; - 6} \right)\). Khi đó góc giữa chúng là

Ký hiệu nào sau đây là để chỉ \(\sqrt 5 \)  không phải là số hữu tỉ ?

Cho các vectơ $\overrightarrow u = \left( {{u_1};{u_2}} \right),{\rm{ }}\overrightarrow v  = \left( {{v_1};{v_2}} \right)$. Điều kiện để vectơ $\overrightarrow u \, = \overrightarrow v $ là

Trong các mệnh đề sau, tìm mệnh đề nào sai ?

Cho mệnh đề \(P \Rightarrow Q\): “Vì \({3^2} + 1\) là số chẵn nên \(3\) là số lẻ”. Chọn mệnh đề đúng:

Số các tập con $3$ phần tử có chứa $\alpha ,\pi $ của \(C = \left\{ {\alpha ,\beta ,\xi ,\pi ,\rho ,\eta ,\gamma ,\sigma ,\omega ,\tau } \right\}\) là:

Cho hai tập hợp $A = \{ 0;1;2;3;4\} ,B = \{ 2;3;4;5;6\} $ . Tập hợp  $\left( {A\backslash B} \right) \cap \left( {B\backslash A} \right)$  bằng :

Miền nghiệm (phần không bị gạch) của bất phương trình \(3x - 2y >  - 6\) là

Cho hệ bất phương trình \(\left\{ \begin{array}{l}x - y \le 2\\3x + 5y \le 15\\x \ge 0\\y \ge 0\end{array} \right.\). Khẳng định nào sau đây là khẳng định sai ?

Nếu $\tan \alpha  + \cot \alpha  = 2$ thì ${\tan ^2}\alpha  + {\rm{ }}{\cot ^2}\alpha $ bằng:

Tam giác $ABC$ có ba cạnh là $6,8,10$ . Khi đó, bán kính đường tròn nội tiếp tam giác $ABC$ là:

Cho tam giác $ABC$ với trực tâm $H$. Gọi $D$ là điểm đối xứng với $B$ qua tâm $O$ của đường tròn ngoại tiếp tam giác $ABC$. Khẳng định nào sau đây là đúng ?

Cho hình chữ nhật $ABCD$ biết $AB = 4a$ và $AD = 3a$ thì độ dài \(\overrightarrow {AB} + \overrightarrow {AD} \) là:

Cho tam giác $ABC$. Gọi \(M\) là điểm trên cạnh $BC$ sao cho $MB = 3MC$. Khi đó, biễu diễn $\overrightarrow {AM} $ theo $\overrightarrow {AB} $ và $\overrightarrow {AC} $ là:

Cho hai vectơ $\overrightarrow a $ và $\overrightarrow b $ không cùng phương. Hai vectơ nào sau đây cùng phương?

Trong mặt phẳng tọa độ \(Oxy\) cho \(\overrightarrow a = (2;1),\overrightarrow {{\rm{ }}b}  = (3;4),{\rm{ }}\overrightarrow c  = (7;2)\). Cho biết \(\overrightarrow c  = m.\overrightarrow a  + n.\overrightarrow b \). Khi đó

Trong mp \(Oxy\) cho \(A\left( {4;6} \right)\), \(B\left( {1;4} \right)\), \(C\left( {7;\dfrac{3}{2}} \right)\). Khẳng định nào sau đây sai

Đề mẫu ĐGNL 2019

Một bác nông dân cần trồng lúa và khoai trên diện tích đất gồm 6 ha, với lượng phân bón dữ trữ là 100kg và sử dụng tối đa 120 ngày công. Để trồng 1 ha lúa cần sử dụng 20kg phân bón, 10 ngày công với lợi nhuận là 30 triệu đồng, để trồng 1 ha khoai cần sử dụng 10 kg phân bón, 30 ngày công với lợi nhuận là 60 triệu đồng. Để đạt được lợi nhuận cao nhất, bác nông dân đã trồng \(x\left( {ha} \right)\) lúa và \(y\left( {ha} \right)\) khoai. Giá trị của \(x\) là:

Cho tam giác $ABC$, tập hợp các điểm $M$ sao cho $\left| {\,\overrightarrow {MA} + \overrightarrow {MB}  + \overrightarrow {MC} \,} \right| = 6$ là:

Gọi M, N lần lượt là trung điểm các cạnh CD, AB của hình bình hành ABCD. Tìm mệnh đề đúng trong các mệnh đề sau:

Tìm $m$ để \(\left[ { - 1;1} \right] \cap \left[ {m - 1;m + 3} \right] \ne \emptyset \)

Cho tam giác $ABC$ vuông tại $A$ có $AB = 5cm,BC = 13cm$. Gọi góc \(\widehat {ABC} = \alpha \) và \(\widehat {ACB} = \beta \) . Hãy chọn kết luận đúng khi so sánh \(\alpha \) và \(\beta \).