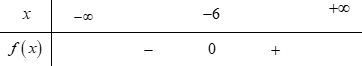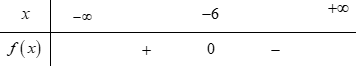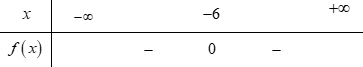Kết quả:
0/50
Thời gian làm bài: 00:00:00
Với giá trị nào của $a$ thì bất phương trình $a{x^2} - x + a \ge 0$ nghiệm đúng với $\forall x \in \mathbb{R}$ ?
Số tổ hợp chập \(k\) của \(n\) phần tử là:
Khoảng cách từ giao điểm của hai đường thẳng \(x - 3y + 4 = 0\) và \(2x + 3y - 1 = 0\) đến đường thẳng $\Delta :3x + y + 4 = 0$ bằng:
Cho biểu thức \(S = C_n^2 + C_n^3 + C_n^4 + C_n^5... + C_n^{n - 2}\). Khẳng định nào sau đây đúng?
Giao điểm của parabol \(\left( P \right)\): \(y = {x^2} + 5x + 4\) với trục hoành:
Phương trình đường thẳng đi qua hai điểm \(A\left( { - 2;4} \right)\,;B\left( { - 6;1} \right)\) là:
Cho đường thẳng \(\left( d \right):3x - 7y + 15 = 0\). Mệnh đề nào sau đây sai?
Chọn ngẫu nhiên một số tự nhiên bé hơn $1000$. Xác suất để số đó chia hết cho $5$ là:
Công việc \(A\) có \(k\) công đoạn \({A_1},{A_2},...,{A_k}\) với số cách thực hiện lần lượt là \({n_1},{n_2},...,{n_k}\). Khi đó số cách thực hiện công việc \(A\) là:
Một đội văn nghệ chuẩn bị được $2$ vở kịch, $3$ điệu múa và $6$ bài hát. Tại hội diễn, mỗi đội chỉ được trình bày \(1\) vở kịch, $1$ điệu múa và \(1\) bài hát. Hỏi đội văn nghệ trên có bao nhiêu cách chọn chương trình diễn, biết chất lượng các vở kịch, các điệu múa, các bài hát là như nhau?
Cho tam giác \(ABC\). Hỏi mệnh đề nào sau đây sai?
Đường tròn có tâm trùng với gốc tọa độ, bán kính \(R = 1\) có phương trình là:
Trong các thí nghiệm sau, thí nghiệm nào không phải là phép thử ngẫu nhiên?
Lập phương trình chính tắc của hypebol $(H)$ biết $(H)$ có tiêu cự bằng $16$ và tâm sai $e = \dfrac{4}{3}$.
Cho \(f\left( x \right) = a{x^2} + bx + c\,\left( {a \ne 0} \right)\). Điều kiện để \(f\left( x \right) \le 0\,,\forall x \in \mathbb{R}\) là
Elip $(E)$ có độ dài trục bé bằng tiêu cự. Tâm sai của $(E)$ là:
Tập nghiệm của phương trình ${x^2} + 3{\rm{x}} + 1 = \left( {x + 3} \right)\sqrt {{x^2} + 1} $ là:
Xét sự biến thiên của hàm số $y = \dfrac{x}{{x - 1}}$. Chọn khẳng định đúng.
Cho \(k,\,\,n\)\(\,(k < n)\) là các số nguyên dương. Mệnh đề nào sau đây SAI?
Bảng xét dấu nào sau đây là của tam thức $f\left( x \right) = \;{x^2} + 12x + 36$?
Xếp ngẫu nhiên $3$ nam và $3$ nữ ngồi vào $6$ ghế xếp thành hàng ngang. Xác suất để nam nữ ngồi xen kẽ nhau là:
Cho đường tròn\((C):{x^2} + {y^2} + 2x + 4y - 20 = 0\). Tìm mệnh đề sai trong các mệnh đề sau:
Khi tịnh tiến parabol \(y = 2{x^2}\) sang trái $3$ đơn vị, ta được đồ thị của hàm số:
Với giá trị nào của \(m\) thì hai đường thẳng \(\left( {{\Delta _1}} \right):3x + 4y - 1 = 0\) và \(\left( {{\Delta _2}} \right):\left( {2m - 1} \right)x + {m^2}y + 1 = 0\) trùng nhau.
Khai triển nhị thức \({\left( {x + 2} \right)^{n + 5}}\,\,\left( {n \in \mathbb{N}} \right)\) có tất cả \(2019\) số hạng. Tìm \(n\).
Phương trình đường tròn $(C)$ đi qua hai điểm \(A(0;1),B(1;0)\) và có tâm nằm trên đường thẳng: \(x + y + 2 = 0\) là:
Gieo hai con súc sắc cân đối và đồng chất. Xác suất để tổng số chấm trên mặt xuất hiện của hai con súc sắc bằng 7 là:
Hàm số nào sau đây có giá trị nhỏ nhất tại $x = \dfrac{3}{4}$?
Cho hàm số: $y = f\left( x \right) = \left| {2x - 3} \right|.$ Tìm \(x\) để$f\left( x \right) = 3.$
Tập nghiệm của phương trình $\sqrt {x + 3} - \sqrt {6 - x} = 3 + \sqrt {\left( {x + 3} \right)\left( {6 - x} \right)} $là:
Hàm số $y = \dfrac{{x + 1}}{{x - 2m + 1}}$ xác định trên $\left[ {0;1} \right)$ khi:
Cho hàm số $y = f(x) = ax^2 + bx +c.$ Rút gọn biểu thức $f(x + 3) – 3f(x + 2) + 3f(x + 1) $ ta được:
Với giá trị nào của $m$ thì bất phương trình ${x^2} - x + m \le 0$ vô nghiệm?
Tổng hai nghiệm của phương trình $5\sqrt x + \dfrac{5}{{2\sqrt x }} = 2{\rm{x}} + \dfrac{1}{{2{\rm{x}}}} + 4$ là:
Cho tam giác \(ABC\) có \(A\left( { - 1; - 2} \right);B\left( {0;2} \right);C\left( { - 2;1} \right)\). Đường trung tuyến \(BM\) có phương trình là:
Lập phương trình đường phân giác trong của góc $A$ của \(\Delta ABC\) biết \(A\left( {2;0} \right);B\left( {4;1} \right);C\left( {1;2} \right)\)
Trong mặt phẳng với hệ tọa độ $Oxy,$ cho $\Delta ABC$ cân có đáy là $BC.$ Đỉnh $A$ có tọa độ là các số dương, hai điểm $B$ và $C$ nằm trên trục $Ox,$ phương trình cạnh $AB:$ $y = 3\sqrt 7 (x - 1)$. Biết chu vi của $\Delta ABC$ bằng $18,$ tìm tọa độ các đỉnh $A,B,C.$
Cho đường tròn ${x^2} + {y^2} - 2x - 6y + 6 = 0$ và điểm $M\left( {4;1} \right).$ Viết phương trình tiếp tuyến của đường tròn và đi qua $M.$
Phương trình chính tắc của elip có một đỉnh là \(B(0; - 2)\), tiêu cự là \(2\sqrt 5 \) là:
Trong mặt phẳng có $2010$ điểm phân biệt sao cho có ba điểm bất kì không thẳng hàng. Hỏi có bao nhiêu véc tơ mà có điểm đầu và điểm cuối phân biệt thuộc $2010$ điểm đã cho.
Một lớp có \(40\) học sinh. Số cách chọn ra \(5\) bạn để làm trực nhật là:
Hệ số của \({x^8}\) trong khai triển biểu thức \({x^2}{\left( {1 + 2x} \right)^{10}} - {x^4}{\left( {3 + x} \right)^8}\) thành đa thức bằng
Một tổ học sinh có \(7\) nam và \(3\) nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được chọn có đúng một người nữ.
Có hai hộp chứa bi. Hộp thứ nhất chứa $4$ viên bi đỏ và $3$ viên bi trắng, hộp thứ hai chứa $2 $ viên bi đỏ và $4$ viên bi trắng. Lấy ngẫu nhiên từ mỗi hộp ra một viên bi, tính xác suất để $2$ viên lấy ra cùng màu.
Trong mặt phẳng với hệ toạ độ $Oxy,$ cho \(\Delta ABC\) có đỉnh $A\left( {1;2} \right),$ phương trình đường trung tuyến \(BM:2x + y + 1 = 0\) và phân giác trong \(CD:x + y - 1 = 0\). Viết phương trình đường thẳng $BC.$
Gọi \(S\) là tập nghiệm của phương trình \(\sqrt {5{x^2} + 4x} - \sqrt {{x^2} - 3x - 18} = 5\sqrt x \). Số phần tử của \(S\) là:
Trong mặt phẳng với hệ trục tọa độ $Oxy,$ cho hai đường thẳng \({d_1}:x + y + 5 = 0,{d_2}:x + 2y - 7 = 0\) và tam giác $ABC$ có \(A(2;3)\), trọng tâm là $G(2;0),$ điểm $B$ thuộc \({d_1}\) và điểm $C$ thuộc \({d_2}\). Viết phương trình đường tròn ngoại tiếp tam giác $ABC.$
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}{x^2} - 2\left| x \right| + 1,x \ne 0\\\,\,\,\,\,\,\,\,\,\,\,\,\,2,\,\,x = 0\end{array} \right.\). Chọn phát biểu đúng?
Cho $n$ là số nguyên dương thỏa mãn điều kiện $6.C_{n\, + \,1}^{n\, - \,1} = A_n^2 + 160.$ Tìm hệ số của ${x^7}$ trong khai triển $\left( {1 - 2{x^3}} \right){\left( {2 + x} \right)^n}.$
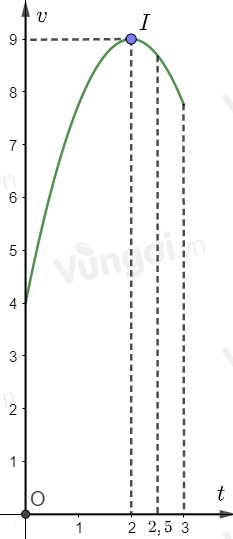
Một vật chuyển động trong 3 giờ với vận tốc \(v\,\,\left( {km/h} \right)\) phụ thuộc thời gian \(t\,\,\left( h \right)\) có đồ thị là một phần của parabol có đỉnh \(I\left( {2;\,\,9} \right)\) và trục đối xứng song song với trục tung như hình vẽ. Vận tốc của vật tại thời điểm 2 giờ 30 phút sau khi vật bắt đầu chuyển động gần bằng giá trị nào nhất trong các giá trị sau?