Đề kiểm tra giữa học kì 1- Đề số 5

Giá trị của biểu thức $S = 3 - {\rm{si}}{{\rm{n}}^2}{\rm{9}}{0^0} + {\rm{ 2co}}{{\rm{s}}^2}{\rm{6}}{{\rm{0}}^0}{\rm{  -  3ta}}{{\rm{n}}^2}{45^0}$ bằng:

Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?

Tập $A = \{ x \in R\left| {1 < x \le 2\} } \right.$ được viết lại dưới dạng đoạn, khoảng là:

Kí hiệu $\overline{\overline P}$ là mệnh đề phủ định của $\overline P$. Khi đó:

Cho hai tập hợp $A{\rm{ }} = \{ 2;{\rm{ }}4;{\rm{ }}6;{\rm{ }}9\} ,{\rm{ }}B{\rm{ }} = \{ 1;{\rm{ }}2;{\rm{ }}3;{\rm{ }}4\}$ . Tập hợp $A{\rm{ }}\backslash {\rm{ }}B$ bằng tập hợp nào sau đây ?

Cho hai tập hợp: $A = \{ x|x$  là ước số nguyên dương của $12\}$

$B = \{ x|\;x$  là ước số nguyên dương của $18\}$

Tập hợp $A \cap B$ là:

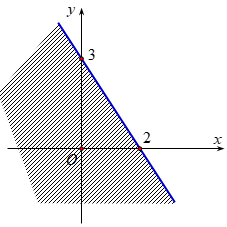
Phần không gạch (không kể d) hình sau là miền nghiệm của bất phương trình nào?

Những tính chất nào sau đây chứng tỏ rằng $B$  là một tập con của $A$ ?

Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình$\left\{ {\begin{array}{*{20}{c}}{2x + 3y - 1 > 0}\\{5x - y + 4 < 0}\end{array}} \right.$?

Cho tập hợp  $A = \left\{ {x \in R|{x^2} + 3x + 4 = 0} \right\}$, kết luận nào sau đây là đúng?

Trong các khẳng định sau khẳng định nào đúng?

Cho các phát biểu sau, hỏi có bao nhiêu phát biểu là mệnh đề ?

1) Hà Nội là thủ đô của Việt Nam.

2) $\forall x \in R,\;5x - {x^2} > 1$.

3) $6x + 1 > 3$.

4) Phương trình ${x^2} + 3x-1 = 0$ có nghiệm.

Trong tam giác $ABC$ có:

Cho mệnh đề $P$: “$35$ là số có hai chữ số”. Mệnh đề $Q$ nào dưới đây thỏa mãn $P \Rightarrow {\rm{Q}}$ là mệnh đề sai?

Trong các mệnh đề sau, tìm mệnh đề nào sai ?

Cho góc $x$  thoả ${0^0} < x < {90^0}$ . Trong các mệnh đề sau, mệnh đề nào sai:

Trong tam giác $ABC$, ta có.

Cho tam giác $ABC$ có $\widehat B = {60^0},\widehat C = {45^0}$ và $AB = 5$. Kết quả nào trong các kết quả sau là độ dài của cạnh $AC$?

Cho hai mệnh đề $P$ và $Q.$ Tìm điều kiện để mệnh đề $P \Leftrightarrow Q$ đúng.

Trong các mệnh đề sau đây, mệnh đề nào đúng?

Mệnh đề $P \Rightarrow Q$ chỉ sai khi:

Trên một tấm bìa cac-tông có ghi 4 mệnh đề sau:

     I. Trên tấm bìa này có đúng một mệnh đề sai.

     II. Trên tấm bìa này có đúng hai mệnh đề sai.

     III. Trên tấm bìa này có đúng ba mệnh đề sai.

     IV. Trên tấm bìa này có đúng bốn mệnh đề sai.

Hỏi trên tấm bìa trên có bao nhiêu mệnh đề sai?

Trong các mệnh đề sau, mệnh đề nào sai ?

Cho tập $A = \left\{ {1;2;3;4;5;6} \right\}$. Số các tập con khác nhau của $A$ gồm hai phần tử là:

Cho 2 tập hợp  $A = \left\{ {x \in R|\left| x \right| > 4} \right\}$, $B = \left\{ {x \in R| - 5 \le x - 1 < 5} \right\}$, chọn mệnh đề sai:

Miền nghiệm (phần không bị gạch) của bất phương trình $3x - 2y >  - 6$ là

Miền biểu diễn nghiệm của hệ bất phương trình $\left\{ \begin{array}{l}y \ge  - 2\\x \ge 2\\2x + y \le 8\end{array} \right.$ có diện tích bằng bao nhiêu?

Biểu thức $A = \dfrac{{\sin \left( { - {{328}^0}} \right).\sin {{958}^0}}}{{\cot {{572}^0}}} - \dfrac{{\cos \left( { - {{508}^0}} \right).\cos \left( { - {{1022}^0}} \right)}}{{\tan \left( { - {{212}^0}} \right)}}$ rút gọn bằng:

Kết quả đơn giản của biểu thức ${\left( {\dfrac{{\sin \alpha  + \tan \alpha }}{{{\rm{cos}}\alpha {\rm{ + 1}}}}} \right)^2} + 1$ bằng:

Tam giác $ABC$ vuông tại $A$, có $AB = c,\;AC = b$. Gọi ${\ell _a}$ là độ dài đoạn phân giác trong góc $\widehat {BAC}$. Tính ${\ell _a}$ theo $b$ và $c$.

Tam giác $ABC$  có $BC = 10$  và $\widehat A = {30^0}$. Khi đó, bán kính đường tròn ngoại tiếp tam giác $ABC$  là:

Cho $A$  là tập hợp các số tự nhiên chẵn không lớn hơn $10$ .

$B = \{ n \in N/n \le 6\}$  và $C = \{ n \in N/4 \le n \le 10\}$ .

Khi đó ta có câu đúng là:

Cho tam giác $ABC$ vuông tại $A$ có $AB = 5cm,BC = 13cm$. Gọi góc $\widehat {ABC} = \alpha$ và $\widehat {ACB} = \beta$ . Hãy chọn kết luận đúng khi so sánh $\alpha$ và $\beta$.

Một công ty Y cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê xe có 2 loại xe, trong đó có 10 xe loại $A$ và 9 xe loại $B$. Một chiếc xe loại $A$ cho thuê với giá 4 triệu, một chiếc xe loại $B$ cho thuê với giá 3 triệu. Biết rằng mỗi xe loại $A$ có thể chở 20 người và 0,6 tấn hàng; mỗi xe loại $B$ có thể chở tối đa 10 người và 1,5 tấn Công ty X cần thuê bao nhiêu xe mỗi loại để chi phí bỏ ra ít nhất?

Giá trị lớn nhất của $6{\cos ^2}x + 6\sin x-2$  là: