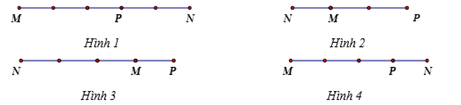Kết quả:
0/50
Thời gian làm bài: 00:00:00
Câu 1
Trắc nghiệm
Trong tam giác ABC, tìm hệ thức sai.
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 2
Trắc nghiệm
Cho tam giác ABC vuông cân tại A có BC=a√2. Tính →CA.→CB
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 3
Trắc nghiệm
Cho tập A≠∅ . Trong các mệnh đề sau, tìm mệnh đề sai ?
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 4
Trắc nghiệm
Cho tam giác ABC có thể xác định được bao nhiêu vectơ (khác vectơ không) có điểm đầu và điểm cuối là đỉnhA,B, C ?
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 5
Trắc nghiệm
Các phát biểu nào sau đây không thể là phát biểu của mệnh đề đúng P⇒Q
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 6
Trắc nghiệm
Trong mặt phẳng Oxy cho →a=(1;3),→b=(−2;1). Tích vô hướng của 2 vectơ →a.→b là:
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 7
Trắc nghiệm
Cho 3 điểm A,B,C phân biệt không thẳng hàng, M là điểm bất kỳ. Mệnh đề nào sau đây đúng?
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 8
Trắc nghiệm
Trên đường thẳng MN lấy điểm P sao cho →MN=−3→MP. Điểm P được xác định đúng trong hình vẽ nào sau đây:
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 9
Trắc nghiệm
Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình{2x+3y−1>05x−y+4<0?
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 10
Trắc nghiệm
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 11
Trắc nghiệm
Cho 4 điểm bất kì A,B,C,O. Đẳng thức nào sau đây đúng?
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 12
Trắc nghiệm
Gọi B là trung điểm của đoạn thẳng AC. Đẳng thức nào sau đây là đúng?
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 13
Trắc nghiệm
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 14
Trắc nghiệm
Trong mặt phẳng tọa độ Oxy, tính khoảng cách giữa hai điểm M(1;−2) và N(−3;4).
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 15
Trắc nghiệm
Ký hiệu nào sau đây là để chỉ 6 là số tự nhiên ?
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 16
Trắc nghiệm
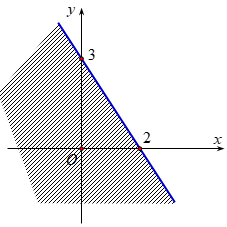
Đẳng thức nào sau đây mô tả đúng hình vẽ bên:
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 17
Trắc nghiệm
Cho vectơ →b≠→0,→a=−2→b,→c=→a+→b. Khẳng định nào sau đây sai?
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 18
Trắc nghiệm
Cho tập hợp A={x∈R|x2+3x+4=0}, kết luận nào sau đây là đúng?
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 19
Trắc nghiệm
Cho hai tập hợp A={0;1;2;3;4},B={1;2;3} . Trong các mệnh đề sau, tìm mệnh đề sai ?
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 20
Trắc nghiệm
Cho vectơ →a. Mệnh đề nào sau đây đúng ?
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 21
Trắc nghiệm
Cho M là trung điểm AB, tìm biểu thức sai:
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 22
Trắc nghiệm
Cho hai tập hợp A={2;4;6;9},B={1;2;3;4} . Tập hợp A∖B bằng tập hợp nào sau đây ?
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 23
Trắc nghiệm
Cho các phát biểu sau, số phát biểu là mệnh đề là:
+) Trái đất hình elip.
+) Các em hãy cố gắng học tập!
+) Một tam giác cân thì mỗi góc đều bằng 600 phải không?
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 24
Trắc nghiệm
Cho bất phương trình 2x+3y−6≤0(1). Chọn khẳng định đúng trong các khẳng định sau
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 25
Trắc nghiệm
Cho các mệnh đề:
(1) “√2 là số hữu tỉ”.
(2) “5 không chia hết cho 3”.
(3) “Tam giác có tổng số đo các góc bằng 1800”.
(4) “Hình vuông có bốn góc bằng nhau”.
Số mệnh đề có mệnh đề phủ định là mệnh đề đúng là:
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 26
Trắc nghiệm
Trong các khẳng định sau, khẳng định nào sai?
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 27
Trắc nghiệm
Cho các phát biểu sau, hỏi có bao nhiêu phát biểu là mệnh đề ?
1) Hà Nội là thủ đô của Việt Nam.
2) ∀x∈R,5x−x2>1.
3) 6x+1>3.
4) Phương trình x2+3x−1=0 có nghiệm.
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 28
Trắc nghiệm
Khẳng định nào trong các khẳng định sau là đúng?
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 29
Trắc nghiệm
Cho điểm M(−3;1), khi đó:
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 30
Trắc nghiệm
Cho bất phương trình bậc nhất hai ẩn x+2y≥0.
Với y=0, có bao nhiêu giá trị của x thỏa mãn bất phương trình đã cho?
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 31
Trắc nghiệm
Cho tam giác ABC có b=10,c=16 và góc ˆA=600. Kết quả nào trong các kết quả sau là độ dài của cạnh BC?
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 32
Trắc nghiệm
Cho →a=(x;2),→b=(−5;1),→c=(x;7). Vec tơ →c=2→a+3→b nếu:
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 33
Trắc nghiệm
Cho góc x thoả 00<x<900 . Trong các mệnh đề sau, mệnh đề nào sai:
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 34
Trắc nghiệm
Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 35
Trắc nghiệm
Gọi Bn là tập hợp bội số của n trong N . Tập hợp B3∪B6 là:
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 36
Trắc nghiệm
Cho A=[a;a+1) . Lựa chọn phương án đúng.
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 37
Trắc nghiệm
Miền nghiệm (phần không bị gạch) của bất phương trình 3x - 2y > - 6 là
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 38
Trắc nghiệm
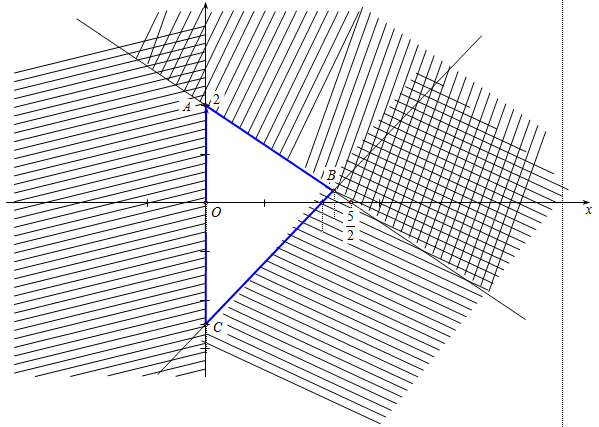
Miền tam giác ABC kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn bệ A, B, C, D ?
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 39
Trắc nghiệm
Nếu \tan \alpha + \cot \alpha = 2 thì {\tan ^2}\alpha + {\rm{ }}{\cot ^2}\alpha bằng:
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 40
Trắc nghiệm
Cho tam giác ABC có AB = 4cm,BC = 7cm,CA = 9cm. Giá trị \cos A là:
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 41
Trắc nghiệm
Cho tứ giác ABCD. Gọi M,N,P,Q lần lượt là trung điểm của AB,BC,CD,DA. Trong các khẳng định sau, hãy tìm khẳng định sai?
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 42
Trắc nghiệm
Cho 6 điểm A,B,C,D,E,F. Đẳng thức nào sau đây đúng.
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 43
Trắc nghiệm
Cho tam giác ABC, điểm M thoả mãn: 5\overrightarrow {MA} = 2\overrightarrow {MB} . Với mỗi điểm I bất kì, nếu \overrightarrow {IA} = m\overrightarrow {IM} + n\overrightarrow {IB} thì cặp số \left( {m;n} \right) bằng:
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 44
Trắc nghiệm
Trong mặt phẳng tọa độ Oxy cho \overrightarrow a = (2;1),\overrightarrow {{\rm{ }}b} = (3;4),{\rm{ }}\overrightarrow c = (7;2). Cho biết \overrightarrow c = m.\overrightarrow a + n.\overrightarrow b . Khi đó
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 45
Trắc nghiệm
Cho tam giác ABC có cạnh BC = 6 và đường cao AH\left( {H \in BC} \right) sao cho BH = 2HC. Tính \overrightarrow {AB} .\overrightarrow {BC}
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 46
Trắc nghiệm
Đề mẫu ĐGNL 2019
Một bác nông dân cần trồng lúa và khoai trên diện tích đất gồm 6 ha, với lượng phân bón dữ trữ là 100kg và sử dụng tối đa 120 ngày công. Để trồng 1 ha lúa cần sử dụng 20kg phân bón, 10 ngày công với lợi nhuận là 30 triệu đồng, để trồng 1 ha khoai cần sử dụng 10 kg phân bón, 30 ngày công với lợi nhuận là 60 triệu đồng. Để đạt được lợi nhuận cao nhất, bác nông dân đã trồng x\left( {ha} \right) lúa và y\left( {ha} \right) khoai. Giá trị của x là:
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 47
Trắc nghiệm
Giá trị của a mà \left[ {a;\dfrac{{a + 1}}{2}} \right] \subset \left(( - \infty ; - 1) \cup (1; + \infty )\right) là
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 48
Trắc nghiệm
Cho tam giác ABC. Tập hợp những điểm M sao cho: \left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MC} + \overrightarrow {MB} } \right| là:
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 49
Trắc nghiệm
Cho tam giác ABC vuông tại A có AB = 5cm,BC = 13cm. Gọi góc \widehat {ABC} = \alpha và \widehat {ACB} = \beta . Hãy chọn kết luận đúng khi so sánh \alpha và \beta .
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 50
Trắc nghiệm
Gọi M, N lần lượt là trung điểm các cạnh CD, AB của hình bình hành ABCD. Tìm mệnh đề đúng trong các mệnh đề sau:
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a