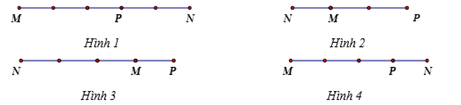Kết quả:
0 /49 Thời gian làm bài: 00:00:00
Câu 1
Trắc nghiệm
Chọn phương án trả lời đúng trong các phương án đã cho sau đây.
Mệnh đề "\(\exists x \in \mathbb{R}:{x^2} = 2\)" khẳng định rằng:
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 2
Trắc nghiệm
Cho tập $A \ne \emptyset $ . Trong các mệnh đề sau, tìm mệnh đề sai ?
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 3
Tự luận
Mẫu số liệu sau cho biết chiều cao (đơn vị cm) của các bạn trong tổ:
163 159 172 167 165 168 170 161
Khoảng biến thiên của mẫu số liệu này là:
Câu hỏi tự luận
Bạn chưa làm câu này
Mẫu số liệu sau cho biết chiều cao (đơn vị cm) của các bạn trong tổ:
163 159 172 167 165 168 170 161
Khoảng biến thiên của mẫu số liệu này là:
Câu 4
Trắc nghiệm
Trong mặt phẳng $Oxy$, cho $B\left( {5; - 4} \right),C\left( {3;7} \right)$. Tọa độ của điểm $E$ đối xứng với $C$ qua $B$ là
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 5
Trắc nghiệm
Tam giác \(ABC\) có đoạn thẳng nối trung điểm của \(AB\) và \(BC\) bằng \(3\), cạnh \(AB = 9\) và \(\widehat {ACB} = 60^\circ \). Tính độ dài cạnh cạnh \(BC\).
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 6
Trắc nghiệm
Với \(\overrightarrow {DE} \) (khác vectơ - không) thì độ dài đoạn \(ED\) được gọi là
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 7
Trắc nghiệm
Cho \(\overrightarrow a = m\overrightarrow i + n\overrightarrow j \) thì tọa độ véc tơ \(\overrightarrow a \) là:
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 8
Trắc nghiệm
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 9
Trắc nghiệm
Cho $3$ điểm \(A\),\(B\),\(C\) phân biệt không thẳng hàng, $M$ là điểm bất kỳ. Mệnh đề nào sau đây đúng ?
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 10
Trắc nghiệm
Nếu \(G\) là trọng tam giác $ABC$ thì đẳng thức nào sau đây đúng.
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 11
Trắc nghiệm
Cho góc \(x\) thoả ${0^0} < x < {90^0}$ . Trong các mệnh đề sau, mệnh đề nào sai :
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 12
Trắc nghiệm
Tập \(A = \{ x \in R\left| {1 < x \le 2\} } \right.\) được viết lại dưới dạng đoạn, khoảng là:
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 13
Trắc nghiệm
Chiều dài một cái cầu là \(l= 1745,25 m ± 0,01 m\). Số quy tròn của số gần đúng \(1745,25\) là
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 14
Trắc nghiệm
Trong tam giác $ABC$, tìm hệ thức sai .
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 15
Trắc nghiệm
Trên đường thẳng $MN$ lấy điểm $P$ sao cho \(\overrightarrow {MN} = - 3\overrightarrow {MP} \). Điểm $P$ được xác định đúng trong hình vẽ nào sau đây:
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 16
Trắc nghiệm
Cho hình vuông $ABCD$, tính ${\rm{cos}}\left( {\overrightarrow {AB} ,\overrightarrow {CA} } \right)$
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 17
Trắc nghiệm
Câu nào sau đây không phải là mệnh đề?
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 18
Trắc nghiệm
Trong các khẳng định sau khẳng định nào đúng ?
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 19
Trắc nghiệm
Cho tam giác $ABC$ với trung tuyến $AM$ và trọng tâm $G$. Khi đó $\overrightarrow {GA} = $
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 20
Trắc nghiệm
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 21
Trắc nghiệm
Cho bất phương trình \(2x + 3y - 6 \le 0\,\,(1)\). Chọn khẳng định đúng trong các khẳng định sau
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 22
Trắc nghiệm
Cho hình vuông \(ABCD\) tâm \(O\). Hỏi mệnh đề nào sau đây sai?
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 23
Trắc nghiệm
Cho hai mệnh đề \(P,Q\), chọn mệnh đề đúng:
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 24
Trắc nghiệm
Cho 3 điểm$A,{\rm{ }}B,{\rm{ }}C$. Đẳng thức nào sau đây đúng.
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 25
Trắc nghiệm
Cho hai tập hợp $A = \{ 0;1;2;3;4\} ,B = \{ 1;2;3\} $ . Trong các mệnh đề sau, tìm mệnh đề sai ?
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 26
Trắc nghiệm
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 27
Trắc nghiệm
Ký hiệu nào sau đây là để chỉ $6$ là số tự nhiên ?
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 28
Trắc nghiệm
Cho điểm \(M\left( { - 3;1} \right)\), khi đó:
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 29
Trắc nghiệm
Cho mệnh đề \(P\): “\(35\) là số có hai chữ số”. Mệnh đề \(Q\) nào dưới đây thỏa mãn \(P \Rightarrow {\rm{Q}}\) là mệnh đề sai?
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 30
Trắc nghiệm
Cho tam giác đều $ABC$ cạnh $a$. Khi đó $\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = $
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 31
Trắc nghiệm
Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình$\left\{ {\begin{array}{*{20}{c}}{2x + 3y - 1 > 0}\\{5x - y + 4 < 0}\end{array}} \right.$?
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 32
Trắc nghiệm
Mệnh đề nào sau đây đúng?
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 33
Trắc nghiệm
Xác định tính đúng sai của mệnh đề sau và tìm phủ định của nó :
F: " \(\exists a \in \mathbb{R}\): \(a + 1 + \dfrac{1}{{a + 1}} \le 2\)"
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 34
Trắc nghiệm
Gọi ${B_n}$ là tập hợp bội số của $n$ trong $N$ . Tập hợp ${B_3} \cap {B_6}$ là:
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 35
Trắc nghiệm
Cho 2 tập hợp $A = \left\{ {x \in R|\left| x \right| > 4} \right\}$, $B = \left\{ {x \in R| - 5 \le x - 1 < 5} \right\}$, chọn mệnh đề sai:
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 36
Trắc nghiệm
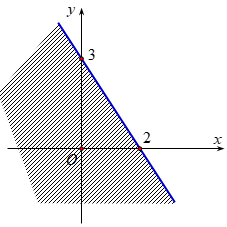
Miền nghiệm (phần không bị gạch) của bất phương trình \(3x - 2y > - 6\) là
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 37
Trắc nghiệm
Cho hệ bất phương trình \(\left\{ \begin{array}{l}2x - \dfrac{3}{2}y \ge 1\\4x - 3y \le 2\end{array} \right.\) có tập nghiệm \(S\). Khẳng định nào sau đây là khẳng định đúng?
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 38
Trắc nghiệm
Rút gọn biểu thức ${\rm{S}} = \cos {\rm{(9}}{{\rm{0}}^0} - x)\sin \left( {{{180}^0} - x} \right) $ $- {\rm{\sin (9}}{{\rm{0}}^0} - x)\cos \left( {{{180}^0} - x} \right)$ ta được kết quả:
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 39
Trắc nghiệm
Tam giác $ABC$ có $BC = 10$ và \(\widehat A = {30^0}\). Khi đó, bán kính đường tròn ngoại tiếp tam giác $ABC$ là:
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 40
Trắc nghiệm
Cho hình thang $ABCD$ có \(AB\) song song với \(CD\). Cho $AB = 2a;CD = a$. Gọi \(O\) là trung điểm của \(AD\). Khi đó :
Bạn đã chọn sai
| Đáp án đúng:
d
Bạn đã chọn đúng
| Đáp án đúng:
d
Bạn chưa làm câu này
| Đáp án đúng:
d
Câu 41
Trắc nghiệm
Hãy chọn kết quả đúng khi phân tích vectơ $\overrightarrow {AM} $ theo hai véctơ $\overrightarrow {AB} $ và $\overrightarrow {AC} $ của tam giác \(ABC\) với trung tuyến $AM$.
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 42
Trắc nghiệm
Trong mặt phẳng $Oxy$, gọi $B',B''$ và $B'''$ lần lượt là điểm đối xứng của $B\left( { - 2;7} \right)$ qua trục $Ox$,$Oy$ và qua gốc tọa độ $O$. Tọa độ của các điểm $B',\,B''$ và $B'''$ là:
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 43
Trắc nghiệm
Cho hình thang vuông \(ABCD\) có đáy lớn \(AB = 4a\), đáy nhỏ \(CD = 2a\), đường cao \(AD = 3a\); \(I\) là trung điểm của \(AD\) . Khi đó \(\left( {\overrightarrow {IA} + \overrightarrow {IB} } \right).\overrightarrow {ID} \) bằng :
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 44
Trắc nghiệm
Bảng sau đây cho biết số lần học tiếng Anh trên internet trong một tuần của một số học sinh lớp 10:
Hãy tìm các tứ phân vị cho mẫu số liệu này.
Các tứ phân vị \({Q_1};{\mkern 1mu} {Q_2};{\mkern 1mu} {Q_3}\) của mẫu số liệu này lần lượt là:
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 45
Trắc nghiệm
Cho tam giác $ABC$ vuông tại $A$ có $AB = 5cm,BC = 13cm$. Gọi góc \(\widehat {ABC} = \alpha \) và \(\widehat {ACB} = \beta \) . Hãy chọn kết luận đúng khi so sánh \(\alpha \) và \(\beta \).
Bạn đã chọn sai
| Đáp án đúng:
b
Bạn đã chọn đúng
| Đáp án đúng:
b
Bạn chưa làm câu này
| Đáp án đúng:
b
Câu 46
Trắc nghiệm
Cho tam giác $ABC$. Tập hợp những điểm \(M\) sao cho: \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MC} + \overrightarrow {MB} } \right|\) là:
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 47
Trắc nghiệm
Tìm $m$ để \(\left[ { - 1;1} \right] \cap \left[ {m - 1;m + 3} \right] \ne \emptyset \)
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c
Câu 48
Trắc nghiệm
Gọi M, N lần lượt là trung điểm các cạnh CD, AB của hình bình hành ABCD. Tìm mệnh đề đúng trong các mệnh đề sau:
Bạn đã chọn sai
| Đáp án đúng:
a
Bạn đã chọn đúng
| Đáp án đúng:
a
Bạn chưa làm câu này
| Đáp án đúng:
a
Câu 49
Trắc nghiệm
Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa $24$ $g$ hương liệu, $9$ lít nước và $210$ $g$ đường để pha chế nước cam và nước táo.
+ Để pha chế $1$ lít nước cam cần $30$ $g$ đường, $1$ lít nước và $1$ $g$ hương liệu;
+ Để pha chế $1$ lít nước táo cần $10$ $g$ đường, $1$ lít nước và $4$ $g$ hương liệu.
Mỗi lít nước cam nhận được $60$ điểm thưởng, mỗi lít nước táo nhận được $80$ điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?
Bạn đã chọn sai
| Đáp án đúng:
c
Bạn đã chọn đúng
| Đáp án đúng:
c
Bạn chưa làm câu này
| Đáp án đúng:
c