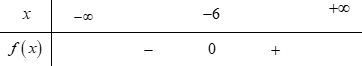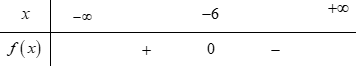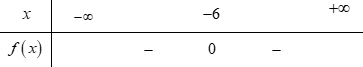Kết quả:
0/25
Thời gian làm bài: 00:00:00
Tập nghiệm của bất phương trình $\left( {2x + 8} \right)\left( {1 - x} \right) > 0$ có dạng $\left( {a;b} \right).$ Khi đó $b - a$ bằng
Cho hàm số \(f\left( x \right) = \sqrt {1 - {x^2}} \). Kết luận nào sau đây đúng?
Có bao nhiêu giá trị thực của tham số \(m\) để bất phương trình $\left( {{m^2} - m} \right)x < m$ vô nghiệm.
Bất phương trình $\left( {m - 1} \right)x > 3$ vô nghiệm khi
Cho bất phương trình \(3{x^2} + x > 0\), giá trị nào của \(x\) dưới đây không thuộc tập nghiệm của bất phương trình?
Cho \(f\left( x \right) = a{x^2} + bx + c\,\left( {a \ne 0} \right)\). Điều kiện để \(f\left( x \right) \le 0\,,\forall x \in \mathbb{R}\) là
Tìm $m$ để $f\left( x \right) = {x^2} - 2\left( {2m - 3} \right)x + 4m - 3 > 0,\;\;\forall x \in \mathbb{R}$?
Bảng xét dấu nào sau đây là của tam thức $f\left( x \right) = \;{x^2} + 12x + 36$?
Tìm điều kiện xác định của bất phương trình $\sqrt {\dfrac{{x + 1}}{{{{\left( {x - 2} \right)}^2}}}} < x + 1.$
Cho bất phương trình\( - 2x + \sqrt 3 y + \sqrt 2 \le 0\) có tập nghiệm là \(S\). Khẳng định nào sau đây là khẳng định đúng?
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
Cho biểu thức \(f\left( x \right) = \left( {x + 5} \right)\left( {3 - x} \right).\) Tập hợp tất cả các giá trị của \(x\) thỏa mãn bất phương trình \(f\left( x \right) \le 0\) là
Tập nghiệm của bất phương trình: $-{x^2} + 6x + 7\; \ge 0\;$là:
Tìm mệnh đề đúng?
Cho $a,b,c > 0$. Xét các bất đẳng thức sau:
(I) $\dfrac{a}{b} + \dfrac{b}{a} \ge 2$
(II) $\dfrac{a}{b} + \dfrac{b}{c} + \dfrac{c}{a} \ge 3$
(III) $\left( {a + b} \right)\left( {\dfrac{1}{a} + \dfrac{1}{b}} \right) \ge 4$
Bất đẳng thức nào đúng?
Hệ bất phương trình $\left\{ \begin{array}{l}3x + 4 > x + 9\\1 - 2x \le m - 3x + 1\end{array} \right.$ vô nghiệm khi và chỉ khi:
Cho biểu thức \(f\left( x \right) = \dfrac{{\left( {x + 3} \right)\left( {2 - x} \right)}}{{x - 1}}.\) Tập hợp tất cả các giá trị của \(x\) thỏa mãn bất phương trình \(f\left( x \right) > 0\) là
Tập nghiệm $S = \left[ {0;5} \right]$ là tập nghiệm của bất phương trình nào sau đây ?
Cho hệ bất phương trình \(\left\{ \begin{array}{l}2x - \dfrac{3}{2}y \ge 1\\4x - 3y \le 2\end{array} \right.\) có tập nghiệm \(S\). Khẳng định nào sau đây là khẳng định đúng?
Tập nghiệm của hệ bất phương trình $\left\{ \begin{array}{l}{x^2} - 4x + 3 > 0\\{x^2} - 6x + 8 > 0\end{array} \right.$ là
Số nghiệm của phương trình: $\sqrt {x + 8 - 2\sqrt {x + 7} } = 2 - \sqrt {x + 1 - \sqrt {x + 7} } $ là:
Cho \(a > b > 0\) và \(x = \dfrac{{1 + a}}{{1 + a + {a^2}}}\), \(y = \dfrac{{1 + b}}{{1 + b + {b^2}}}\). Mệnh đề nào sau đây đúng?
Giá trị nhỏ nhất của biết thức $F = y - x$ trên miền xác định bởi hệ $\left\{ {\begin{array}{*{20}{c}}{y - 2x \le 2}\\{2y - x \ge 4}\\{x + y \le 5}\end{array}} \right.$ là.
Tìm tất cả các giá trị của tham số \(m\) để bất phương trình \(mx + 4 > 0\) nghiệm đúng với mọi \(\left| x \right| < 8\).
Cho bất phương trình: ${x^2} - 2x \le \left| {x - 2} \right| + ax - 6$. Giá trị dương nhỏ nhất của $a$ để bất phương trình có nghiệm gần nhất với số nào sau đây: