Đề kiểm tra học kì 1 - Đề số 3

Cho hình bình hành \(ABCD\) tâm \(O\). Khi đó \(\overrightarrow {OA} + \overrightarrow {BO}  = \)

Cho \(K\left( {1; - 3} \right)\). Điểm \(A \in Ox,B \in Oy\) sao cho \(A\) là trung điểm \(KB\). Tọa độ điểm \(B\) là:

Chọn mệnh đề đúng:

Các phát biểu nào sau đây không thể là phát biểu của mệnh đề đúng \(P \Rightarrow Q\)

Trong mặt phẳng tọa độ \(Oxy\) cho \(A\left( {5;2} \right),B\left( {10;8} \right)\). Tọa độ của vec tơ \(\overrightarrow {BA} \) là:

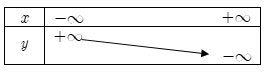
Hàm số $y = \left| x \right| + 2$ có bảng biến thiên nào sau đây?

Cho hai điểm $A\left( {1;0} \right)$ và $B\left( {0; - 2} \right)$. Tọa độ trung điểm của đoạn thẳng $AB$ là:

Điều kiện xác định của phương trình \(x + \dfrac{1}{{\sqrt {2x + 4} }} = \dfrac{{\sqrt {3 - 2x} }}{x}\) là

Tam giác \(ABC\) có đoạn thẳng nối trung điểm của \(AB\) và \(BC\) bằng \(3\), cạnh \(AB = 9\) và \(\widehat {ACB} = 60^\circ \). Tính độ dài cạnh cạnh \(BC\).

Cho tập hợp B = \(\left( { - \infty ; - 2} \right] \cap \left[ { - 2; + \infty } \right)\). Khi đó tập hợp $B$ là:

Ký hiệu nào sau đây là để chỉ $6$ là số tự nhiên ?

Trong mặt phẳng tọa độ \(Oxy,\) cho vectơ \(\overrightarrow a  = \left( {9;3} \right)\). Vectơ nào sau đây không vuông góc với vectơ \(\overrightarrow a \)?  

Cho hình vuông \(ABCD\) tâm \(O\). Hỏi mệnh đề nào sau đây sai?

Cho hàm số:$f(x) = \left\{ \begin{array}{l}\dfrac{x}{{x + 1}},{\rm{ }}x \ge 0\\\dfrac{1}{{x - 1}},{\rm{ }}x < 0\end{array} \right.$. Giá trị $f\left( 0 \right),f\left( 2 \right),f\left( { - 2} \right)$ là

Cho các điểm phân biệt $A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D,{\rm{ }}E,{\rm{ }}F$. Đẳng thức nào sau đây sai ?

Trong hệ tọa độ \(Oxy,\) cho tam giác \(ABC\) có \(A\left( {6;1} \right),{\rm{ }}B\left( { - 3;5} \right)\) và trọng tâm \(G\left( { - 1;1} \right)\). Tìm tọa độ đỉnh \(C\)?

Xét tính đồng biến, nghịch biến của hàm số \(f\left( x \right) = \dfrac{{x - 3}}{{x + 5}}\) trên khoảng \(\left( { - \infty ; - 5} \right)\) và trên khoảng \(\left( { - 5; + \infty } \right)\). Khẳng định nào sau đây đúng?

Giá trị \(\cos {45^0} + \sin {45^0}\) bằng bao nhiêu? 

Cho hình bình hành $ABCD$. Đẳng thức nào sau đây sai.

Số phần tử của tập \(A = \{ {( - 1)^n},n \in {\mathbb{N}^*}\} \) là:

Cho phương trình \(\left( {{x^2} + 1} \right)\left( {x-1} \right)\left( {x + 1} \right) = 0\). Phương trình nào sau đây tương đương với phương trình đã cho?

Hệ phương trình $\left\{ \begin{array}{l}x - y = 9\\x.y = 90\end{array} \right.$ có nghiệm là :

Phương trình sau đây có bao nhiêu nghiệm âm: \({x^6} + 2003{x^3} - 2005 = 0\)

Trong mặt phẳng tọa độ \(Oxy,\) cho ba vectơ \(\overrightarrow a  = \left( {1;2} \right),{\rm{ }}\overrightarrow b  = \left( {4;3} \right)\) và \(\overrightarrow c  = \left( {2;3} \right).\)

Tính \(P = \overrightarrow a .\left( {\overrightarrow b  + \overrightarrow c } \right).\)  

Cho hai tập hợp $X = \left\{ {1;3;5;8} \right\},Y = \left\{ {3;5;7;9} \right\}$ . Tập hợp $X \cup Y$ bằng tập hợp nào sau đây ?

Cho $3$ điểm \(A\),\(B\),\(C\) phân biệt không thẳng hàng, $M$ là điểm bất kỳ. Mệnh đề nào sau đây đúng?

Gọi $S$ là tập hợp tất cả các giá trị nguyên của tham số $m$ thuộc $\left[ { - 20;20} \right]$ để phương trình ${x^2} - 2mx + 144 = 0$ có nghiệm. Tổng của các phần tử trong $S$ bằng:

Xác định parabol \(\left( P \right):y = a{x^2} + bx + 2\), biết rằng \(\left( P \right)\) đi qua hai điểm \(M\left( {1;5} \right)\) và \(N\left( { - 2;8} \right)\).

Cho $A$  là tập hợp các ước nguyên dương của $24,{\rm{ }}B$  là tập hợp các ước nguyên dương của $18$ . Xác định tính sai của các kết quả sau:

Phương trình $a{x^2} + bx + c = 0\left( {a > 0} \right)$ có nghiệm duy nhất khi và chỉ khi:

Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

Tìm giá trị nhỏ nhất của hàm số $f\left( x \right)$ biết rằng $f\left( {x + 2} \right) = {x^2} - 3x + 2$ trên $\mathbb{R}$

Có bao nhiêu giá trị nguyên của $m$ để phương trình:\(2{\left( {{x^2} + 2x} \right)^2} - \left( {4m - 1} \right)\left( {{x^2} + 2x} \right) +  2m -1= 0\) có đúng $3$ nghiệm thuộc \(\left[ { - 3;0} \right].\)

Tổng bình phương các nghiệm của phương trình $\dfrac{2}{{\sqrt {x + 1}  + \sqrt {3 - x} }} = 1 + \sqrt {3 + 2{\rm{x}} - {x^2}} $ là:

Hệ phương trình $\left\{ \begin{array}{l}{x^3} = 3x + 8y\\{y^3} = 3y + 8x\end{array} \right.$ có nghiệm là \(\left( {x;y} \right)\) với \(x \ne 0\) và \(y \ne 0\) là :

Tam giác \(ABC\) có \(AB = AC = a\) và \(\widehat {BAC} = 120^\circ \). Tính \(\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right|.\)

Cho tam giác \(ABC\) và điểm \(M\) thỏa mãn \(\overrightarrow {MA}  = \overrightarrow {MB}  + \overrightarrow {MC} .\) Khẳng định nào sau đây đúng ?

Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC,\,\,\,I\) là trung điểm của \(AM.\) Khẳng định nào sau đây đúng ?

Trong mặt phẳng $Oxy$, cho $A\left( { - 2;0} \right),\;B\left( {5; - 4} \right),\;C\left( { - 5;1} \right)$. Tọa độ điểm $D$ để tứ giác $BCAD$ là hình bình hành là:

Cho \(M\left( {2;0} \right),\,N\left( {2;2} \right),\,P\left( { - 1;3} \right)\) lần lượt là trung điểm các cạnh \(BC,\,CA,\,AB\) của \(\Delta ABC\). Tọa độ \(B\) là:

Giá trị của \(E = \sin {36^0}\cos {6^0}-\sin {126^0}\cos {84^0}\) là

Cho hình thoi \(ABCD\) có \(AC = 8\) và \(BD = 6.\) Tính \(\overrightarrow {AB} .\overrightarrow {AC} .\)

Cho hình vuông \(ABCD\) cạnh \(a.\) Tính \(P = \left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right).\left( {\overrightarrow {BC}  + \overrightarrow {BD}  + \overrightarrow {BA} } \right).\)  

Cho$A\left( {2;\;5} \right),\;B\left( {1;\;3} \right),\;C\left( {5;\; - 1} \right)$. Tìm tọa độ điểm \(K\) sao cho \(\overrightarrow {AK} = 3\overrightarrow {BC}  + 2\overrightarrow {CK} \)

Tam giác \(ABC\) có \(a = 21,{\rm{ }}b = 17,{\rm{ }}c = 10\). Tính bán kính \(r\) của đường tròn nội tiếp tam giác đã cho.

Cho tam giác đều \(ABC\) cạnh \(a.\) Biết rằng tập hợp các điểm \(M\) thỏa mãn đẳng thức \(\left| {2\overrightarrow {MA}  + 3\overrightarrow {MB}  + 4\overrightarrow {MC} } \right| = \left| {\overrightarrow {MB}  - \overrightarrow {MA} } \right|\) là đường tròn cố định có bán kính \(R.\) Tính bán kính \(R\) theo \(a.\)

Cho hai đa thức $f\left( x \right)$ và $g\left( x \right)$ . Xét các tập hợp :

\(\begin{array}{l}A = \left\{ {x \in R|f\left( x \right) = 0} \right\}\\B = \left\{ {x \in R|g\left( x \right) = 0} \right\}\\C = \left\{ {x \in R|\dfrac{{f\left( x \right)}}{{g\left( x \right)}} = 0} \right\}\end{array}\)

Trong các mệnh đề sau, mệnh đề nào đúng ?

Tìm giá trị nhỏ nhất của biểu thức $P = 3\left( {\dfrac{{{a^2}}}{{{b^2}}} + \dfrac{{{b^2}}}{{{a^2}}}} \right) - 8\left( {\dfrac{a}{b} + \dfrac{b}{a}} \right)$.

Định $k$ để phương trình: ${x^2} + \dfrac{4}{{{x^2}}} - 4\left( {x - \dfrac{2}{x}} \right) + k - 1 = 0$ có đúng hai nghiệm lớn hơn $1$.

Cho biết \(\sin \alpha  - \cos \alpha  = \dfrac{1}{{\sqrt 5 }}.\) Giá trị của \(P = \sqrt {{{\sin }^4}\alpha  + {{\cos }^4}\alpha } \) bằng bao nhiêu ?