Đề kiểm tra học kì 1 - Đề số 10

Tập nghiệm của phương trình: $\sqrt {3 - x}  = \sqrt {x + 2}  + 1$

Trong tam giác $ABC$, ta có.

Biết \(\overrightarrow a \), \(\overrightarrow b \)\( \ne \overrightarrow 0 \) và \(\overrightarrow a .\overrightarrow b  =  - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\). Câu nào sau đây đúng

Cho tập hợp \(A = \left\{ {1;2;3;4;5} \right\}\). Mệnh đề nào sau đây sai?

Cho $A = \left\{ {1;2;3} \right\}$. Trong các khẳng định sau, khẳng định nào sai ?

Cho tam giác đều $ABC$ cạnh $a$. Khi đó $\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = $

Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình$\left\{ {\begin{array}{*{20}{c}}{2x + 3y - 1 > 0}\\{5x - y + 4 < 0}\end{array}} \right.$?

Tìm $m$ để $f\left( x \right) = {x^2} - 2\left( {2m - 3} \right)x + 4m - 3 > 0,\;\;\forall x \in \mathbb{R}$?

Giải bất phương trình \( - 2{x^2} + 3x - 7 \ge 0.\)

Cho hai tập hợp $A{\rm{ }} = \{ 1;{\rm{ }}2;{\rm{ }}3;{\rm{ }}7\} ,{\rm{ }}B{\rm{ }} = \{ 2;{\rm{ }}4;{\rm{ }}6;{\rm{ }}7;{\rm{ }}8\} $ . Khẳng định nào sau đây là đúng ?

Điểm nào sau đây thuộc đồ thị hàm số $y = 2\left| {x-1} \right| + 3\left| x \right| - 2$?

Cho hai tập hợp \(A = \left\{ {1;5} \right\}\) và \(B = \left\{ {1;3;5} \right\}.\) Tìm \(A \cap B.\)

Cho $3$ điểm \(A\),\(B\),\(C\) phân biệt không thẳng hàng, $M$ là điểm bất kỳ. Mệnh đề nào sau đây đúng?

Cho tập $A \ne \emptyset $ . Trong các mệnh đề sau, tìm mệnh đề sai ?

Xác định Parabol $\left( P \right):\,\,y = a{x^2} + bx + 2$ biết rằng Parabol đi qua hai điểm $M\left( {1;\,\,5} \right)$ và $N\left( {2;\,\, - 2} \right)$.

Ký hiệu nào sau đây là để chỉ $6$ là số tự nhiên ?

Kí hiệu \(\overline{\overline P} \) là mệnh đề phủ định của \(\overline P \). Khi đó:

Trên đường thẳng $MN$ lấy điểm $P$ sao cho \(\overrightarrow {MN} =  - 3\overrightarrow {MP} \). Điểm $P$ được xác định đúng trong hình vẽ nào sau đây:

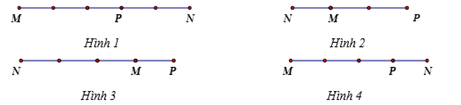
Phần không gạch (không kể d) hình sau là miền nghiệm của bất phương trình nào?

Tìm các giá trị của m để hàm số $y = {x^2} + mx + 5$ luôn đồng biến trên $\left( {1;\,\, + \infty } \right)$.

Khi tịnh tiến parabol \(y = 2{x^2}\) sang trái $3$ đơn vị, ta được đồ thị của hàm số:

Xét sự biến thiên của hàm số $y = \dfrac{x}{{x - 1}}$. Chọn khẳng định đúng.

Chọn phương án trả lời đúng trong các phương án đã cho sau đây.

Mệnh đề "\(\exists x \in \mathbb{R}:{x^2} = 2\)" khẳng định rằng:

Cho hai mệnh đề \(P\) và \(Q.\) Phát biểu nào sau đây sai về mệnh đề đúng \(P \Leftrightarrow Q\) ?

Cho hai mệnh đề \(P\) và \(Q\) là các mệnh đề phủ định của nhau. Chọn mệnh đề đúng:

Cho tam giác $ABC$ có \(\widehat B = {60^0},\widehat C = {45^0}\) và $AB = 5$. Kết quả nào trong các kết quả sau là độ dài của cạnh $AC$?

Cho tam giác $ABC$ có trọng tâm $G$ và trung tuyến $AM$. Khẳng định nào sau đây là sai:

Trong các khẳng định sau, khẳng định nào đúng?

Tam giác $ABC$  có $BC = a,CA = b,AB = c$  và có diện tích $S$ . Nếu tăng cạnh $BC$  lên $2$  lần đồng thời tăng cạnh $CA$  lên $3$  lần và giữ nguyên độ lớn của góc $C$  thì khi đó diện tích tam giác mới được tạo nên bằng:

Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?

Cho tam giác \(ABC\) có thể xác định được bao nhiêu vectơ (khác vectơ không) có điểm đầu và điểm cuối là đỉnh\(A\),\(B\), \(C\) ?

Phương trình: $\sqrt {x - 1}  = x - 3$ có tập nghiệm là:

Cho \(f\left( x \right) = a{x^2} + bx + c\,{\rm{ }}\left( {a \ne 0} \right).\) Điều kiện để \(f\left( x \right) > 0\,,{\rm{ }}\forall x \in \mathbb{R}\) là

Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

Tìm $m$ để \(\left( {0;1} \right) \cap \left( {m;m + 3} \right) = \emptyset \)

Ông An muốn thuê một chiếc ô tô (có lái xe) trong một tuần. Giá thuê xe được cho như bảng sau:

Giả sử, từ thứ Hai đến thứ Sáu, tổng số kilômét ông An đi là x (km) và trong hai ngày cuối tuần, tổng số kilômét ông An đi là y (km). Viết bất phương trình biểu thị mối liên hệ giữa x và y sao cho

tổng số tiền ông An phải trả không quá 14 triệu đồng.

Trong các hàm số sau, hàm số nào tăng trên khoảng $\left( { - 1;0} \right)$?

Cho  phương trình của $\left( P \right):\,\,y = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)$ biết rằng hàm số  có giá trị lớn nhất bằng 1 và đồ thị hàm số đi qua các điểm $A\left( {2;\,\,0} \right),\,\,B\left( { - 2;\,\, - 8} \right)$. Tình tổng ${a^2} + {b^2} + {c^2}$.

Tìm \(m\) để hệ \(\left\{ \begin{array}{l}{x^2} - 2x + 1 - m \le 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\{x^2} - \left( {2m + 1} \right)x + {m^2} + m \le 0\,\,\,\left( 2 \right)\end{array} \right.\) có nghiệm.

Tập nghiệm \(S\) của bất phương trình \(\dfrac{{ - \,2{x^2} + 7x + 7}}{{{x^2} - 3x - 10}} \le  - 1\) là

Cho phương trình $2{{\rm{x}}^2} + 3{\rm{x}} - 14 = 2\sqrt[3]{{2{{\rm{x}}^2} + 3{\rm{x}} - 10}}$ . Giả sử ${x_1},{x_2}$  là 2 nghiệm của phương trình. Tính giá trị biểu thức $A = \sqrt {{x_1}^2 + {x_2}^2 - 4{{\rm{x}}_1}.{x_2}} $

Cho tam giác $ABC$  có $AB = 8cm,AC = 18cm$ và có diện tích bằng \(64c{m^2}\). Giá trị $\sin \widehat A$  là:

Cho lục giác đều $ABCDEF$ tâm $O$. Ba vectơ bằng vecto \(\overrightarrow {BA} \) là:

Cho hình thang $ABCD$ có \(AB\) song song với \(CD\). Cho $AB = 2a;CD = a$. Gọi \(O\) là trung điểm của \(AD\). Khi đó :

Biết rằng hai vec tơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương nhưng hai vec tơ \(2\overrightarrow a - 3\overrightarrow b \) và \(\overrightarrow a  + \left( {x - 1} \right)\overrightarrow b \) cùng phương. Khi đó giá trị của \(x\) là:

Giá trị nhỏ nhất của biết thức $F = y - x$ trên miền xác định bởi hệ $\left\{ {\begin{array}{*{20}{c}}{y - 2x \le 2}\\{2y - x \ge 4}\\{x + y \le 5}\end{array}} \right.$ là.

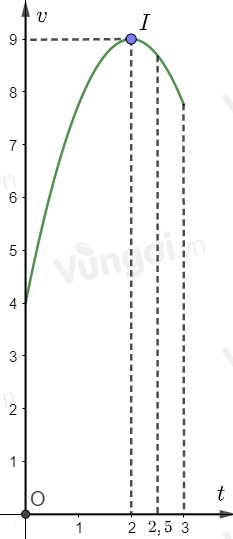
Một vật chuyển động trong 3 giờ với vận tốc  \(v\,\,\left( {km/h} \right)\) phụ thuộc thời gian \(t\,\,\left( h \right)\)  có đồ thị là một phần của parabol có đỉnh \(I\left( {2;\,\,9} \right)\) và trục đối xứng song song với trục tung như hình vẽ. Vận tốc của vật tại thời điểm 2 giờ 30 phút sau khi vật bắt đầu chuyển động gần bằng giá trị nào nhất trong các giá trị sau?

Gọi M, N lần lượt là trung điểm các cạnh CD, AB của hình bình hành ABCD. Tìm mệnh đề đúng trong các mệnh đề sau:

Tập nghiệm của bất phương trình \(\left( {\sqrt {2x + 4}  - \sqrt {x + 1} } \right)\left( {\sqrt {2x + 1}  + \sqrt {x + 4} } \right) \le x + 3\) là tập con của tập hợp nào sau đây?

Giá trị lớn nhất của $6{\cos ^2}x + 6\sin x-2$  là: