Đề kiểm tra học kì 1 - Đề số 9

Cho \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ cùng hướng và đều khác vectơ \(\overrightarrow 0 \). Trong các kết quả sau đây, hãy chọn kết quả đúng:

Mệnh đề đảo của mệnh đề “Ba số tự nhiên liên tiếp thì có tổng chia hết cho \(3\)” được phát biểu là:

Tâp hợp \(\left[ {0;4} \right] \cap \left[ {3;5} \right] \) là

Cho hàm số: $y = f\left( x \right) = \left| {2x - 3} \right|.$ Tìm \(x\) để$f\left( x \right) = 3.$

Cho $A$  là tập hợp các ước nguyên dương của $24,{\rm{ }}B$  là tập hợp các ước nguyên dương của $18$ . Xác định tính sai của các kết quả sau:

Tìm mệnh đề đúng

Tập nghiệm của bất phương trình: $-{x^2} + 6x + 7\; \ge 0\;$là:

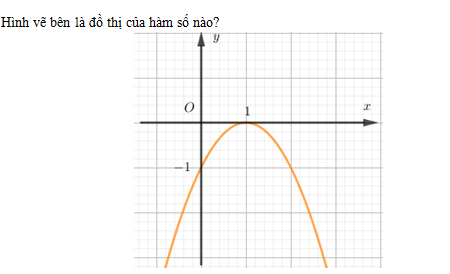
Cho tam giác $ABC$  có $b = 10,c = 16$  và góc \(\widehat A = {60^0}\). Kết quả nào trong các kết quả sau là độ dài của cạnh $BC$?

Tìm giá trị của $m$ để hàm số $y =  - {x^2} + 2x + m - 5$ đạt giá trị lớn nhất bằng $6$

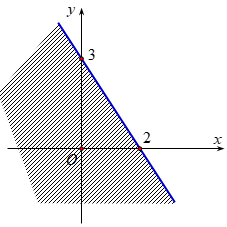
Phần không gạch (không kể d) hình sau là miền nghiệm của bất phương trình nào?

Kí hiệu \(\overline{\overline P} \) là mệnh đề phủ định của \(\overline P \). Khi đó:

Cho $A = \left\{ {1;2;3} \right\}$. Trong các khẳng định sau, khẳng định nào sai ?

Cho đồ thị hàm số $y = a{x^2} + bx + c\,$như hình vẽ.

Khẳng định nào sau đây là đúng:

Biết parabol $(P): y = ax^2+ 2x + 5$ đi qua điểm $A(2; 1).$ Giá trị của $a$ là:

Cho tam giác đều \(ABC\) cạnh \(a = 2\). Hỏi mệnh đề nào sau đây sai?

Xét sự biến thiên của hàm số $y = \dfrac{x}{{x - 1}}$. Chọn khẳng định đúng.

Tam giác $ABC$  có $BC = a,CA = b,AB = c$  và có diện tích $S$ . Nếu tăng cạnh $BC$  lên $2$  lần đồng thời tăng cạnh $CA$  lên $3$  lần và giữ nguyên độ lớn của góc $C$  thì khi đó diện tích tam giác mới được tạo nên bằng:

Gọi $C$ là trung điểm của đoạn $AB$. Hãy chọn khẳng định đúng trong các khẳng định sau :

Chọn phương án trả lời đúng trong các phương án đã cho sau đây.

Mệnh đề "\(\exists x \in \mathbb{R}:{x^2} = 2\)" khẳng định rằng:

Với giá trị nào của $a$ thì bất phương trình $a{x^2} - x + a \ge 0$ nghiệm đúng với $\forall x \in \mathbb{R}$ ?

Cho \(f\left( x \right) = a{x^2} + bx + c\,{\rm{ }}\left( {a \ne 0} \right).\) Điều kiện để \(f\left( x \right) > 0\,,{\rm{ }}\forall x \in \mathbb{R}\) là

Gọi $B$ là trung điểm của đoạn thẳng $AC$. Đẳng thức nào sau đây là đúng?

Phát biểu nào là sai?

Cho bất phương trình bậc nhất hai ẩn \(x + 2y \ge 0\).

Với y=0, có bao nhiêu giá trị của x thỏa mãn bất phương trình đã cho?

Chọn khẳng định sai

Tập nghiệm của phương trình $\sqrt {3{{\rm{x}}^2} + 6{\rm{x}} + 16}  + \sqrt {{{\rm{x}}^2} + 2{\rm{x}}}  = 2\sqrt {{{\rm{x}}^2} + 2{\rm{x}} + 4} $ là:

Để tính $cos{120^0}$ , một học sinh làm như sau:

$(I)\sin {120^0} = \dfrac{{\sqrt 3 }}{2} \Rightarrow (II){\cos ^2}{120^0} = 1 - {\sin ^2}{120^0} \Rightarrow (III){\cos ^2}{120^0} = \dfrac{1}{4} \Rightarrow (IV)\cos {120^0} = \dfrac{1}{2}$

Lập luận trên sai từ bước nào?

Cho ba điểm $M,N,P$ thẳng hàng, trong đó điểm $N$ nằm giữa hai điểm $M$ và $P$. Khi đó các cặp vecto nào sau đây cùng hướng ?

Cho tập hợp  \(A = \left\{ {x \in R|{x^2} + 3x + 4 = 0} \right\}\), kết luận nào sau đây là đúng?

Trên đường thẳng $MN$ lấy điểm $P$ sao cho \(\overrightarrow {MN} =  - 3\overrightarrow {MP} \). Điểm $P$ được xác định đúng trong hình vẽ nào sau đây:

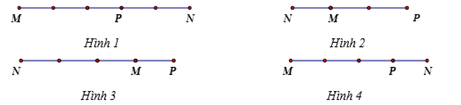
Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

Xác định tính đúng sai của mệnh đề sau và tìm phủ định của nó :

F: " \(\exists  a \in \mathbb{R}\):  \(a + 1 + \dfrac{1}{{a + 1}} \le 2\)"

Cho tập  hợp $A = \left\{ {x \in R|{x^4}-6{x^2} + 8 = 0} \right\}$ . Số phần tử của tập $A$  là:

Cho hai tập hợp $A = \{ 0;1;2;3;4\} ,B = \{ 2;3;4;5;6\} $ . Tập hợp  $\left( {A\backslash B} \right) \cap \left( {B\backslash A} \right)$  bằng :

Miền nghiệm (phần không bị gạch) của bất phương trình \(3x - 2y >  - 6\) là

Tìm tất cả giá trị thực của tham số \(m\) để hệ bất phương trình \(\left\{ \begin{array}{l}{x^2} + 10x + 16 \le 0\left( 1 \right)\\mx \ge 3m + 1\left( 2 \right)\end{array} \right.\) vô nghiệm.

Hệ bất phương trình $\left\{ \begin{array}{l}{x^2} - 1 \le 0\\x - m > 0\end{array} \right.$ có nghiệm khi

Kết quả đơn giản của biểu thức \({\left( {\dfrac{{\sin \alpha  + \tan \alpha }}{{{\rm{cos}}\alpha {\rm{ + 1}}}}} \right)^2} + 1\) bằng:

Trên sân bóng chày dành cho nam, các vị trí gôn Nhà (Home plate), gôn 1 (First base), gôn 2 (Second base), gôn 3 (Third base) là bốn đỉnh của một hình vuông có cạnh dài 27,4 m. Vị trí đứng ném bóng (Pitcher’s mound) nằm trên đường nối gôn Nhà với gôn 2, và cách gôn Nhà 18,44 m. Tính các khoảng cách từ vị trí đứng ném bóng tới các gôn 1 và gôn 3.

Cho lục giác đều $ABCDEF$ tâm $O$. Ba vectơ bằng vecto \(\overrightarrow {BA} \) là:

Gọi $G$ là trọng tâm tam giác vuông $ABC\;$ với cạnh huyền $BC =  12$. Vectơ $\overrightarrow {GB}  - \overrightarrow {CG} $ có độ dài bằng bao nhiêu?

Cho hai tam giác $ABC$ và $A'B'C'$ lần lượt có trọng tâm là $G$ và $G'$. Đẳng thức nào sau đây là sai?

Gọi M, N lần lượt là trung điểm các cạnh CD, AB của hình bình hành ABCD. Tìm mệnh đề đúng trong các mệnh đề sau:

Tập nghiệm của phương trình $\sqrt {x + 5 - 4\sqrt {x + 1} }  + \sqrt {x + 2 - 2\sqrt {x + 1} }  = 1$ là:

Cho hàm số \(y = m{x^2} - 2\left( {m - 1} \right)x + 1\left( {m \ne 0} \right)\) có đồ thị \(\left( {{C_m}} \right)\). Tịnh tiến \(\left( {{C_m}} \right)\) qua trái \(1\) đơn vị ta được đồ thị hàm số \(\left( {{C_m}'} \right)\). Giá trị của \(m\) để giao điểm của \(\left( {{C_m}} \right)\) và \(\left( {{C_m}'} \right)\) có hoành độ \(x = \dfrac{1}{4}\) thỏa mãn điều kiện nào dưới đây?

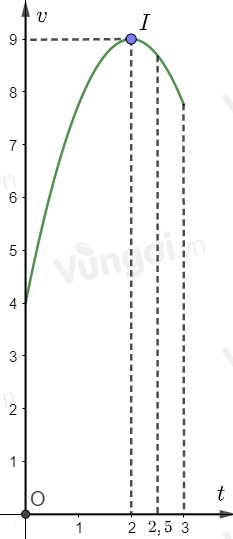
Một vật chuyển động trong 3 giờ với vận tốc  \(v\,\,\left( {km/h} \right)\) phụ thuộc thời gian \(t\,\,\left( h \right)\)  có đồ thị là một phần của parabol có đỉnh \(I\left( {2;\,\,9} \right)\) và trục đối xứng song song với trục tung như hình vẽ. Vận tốc của vật tại thời điểm 2 giờ 30 phút sau khi vật bắt đầu chuyển động gần bằng giá trị nào nhất trong các giá trị sau?

Tìm giá trị nhỏ nhất của biểu thức $P = 3\left( {\dfrac{{{a^2}}}{{{b^2}}} + \dfrac{{{b^2}}}{{{a^2}}}} \right) - 8\left( {\dfrac{a}{b} + \dfrac{b}{a}} \right)$.

Một công ty kinh chuẩn bị cho đợt khuyến mại nhằm mục đích thu hút khác hàng bằng cách tiến hành quảng cáo sản phẩm của công ty trên internet và truyền hình. Chi phí cho 1 phút quảng cáo trên internet là 800.000 đồng, trên sóng truyền hình là 4.000.000 đồng. Trang internet chỉ nhận phát các chương trình quảng cáo ngắn nhất là 5 phút. Do nhu cầu quảng cáo trên truyền hình lớn nên đài truyền hình chỉ nhận phát các chương trình dì tối đa là 4 phút. Theo các phân tích, cùng thời lượng một phút quảng cáo, trên truyền hình sẽ có hiệu quả gấp 6 lần trên internet. Công ty dự định chi tối đa 16.000.000 đồng cho quảng cáo. Công ty cần đặt thời lượng quảng cáo trên internet và truyền hình như thế nào để hiệu quả nhất?