Kết quả:
0/25
Thời gian làm bài: 00:00:00
Khẳng định nào sau đây sai?
Tìm \(m\) để hàm số \(y = - \left( {{m^2} + 1} \right)x + m - 4\) nghịch biến trên \(\mathbb{R}.\)
Cho tập hợp \(A = \left\{ {x \in R|{x^2} + 3x + 4 = 0} \right\}\), kết luận nào sau đây là đúng?
Cho $\overrightarrow a = 3\overrightarrow i - 4\overrightarrow j $ và $\overrightarrow b = \overrightarrow i - \overrightarrow j $. Tìm phát biểu sai:
Câu nào sau đây đúng?
Trong mặt phẳng $Oxy$, cho $B\left( {5; - 4} \right),C\left( {3;7} \right)$. Tọa độ của điểm $E$ đối xứng với $C$ qua $B$ là
Trên đường thẳng $MN$ lấy điểm $P$ sao cho \(\overrightarrow {MN} = - 3\overrightarrow {MP} \). Điểm $P$ được xác định đúng trong hình vẽ nào sau đây:
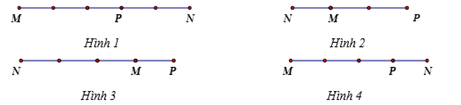
Cho tam giác \(ABC\). Gọi \(M,\,N,\,P\) lần lượt là trung điểm của \(BC,\,CA,\,AB\). Có bao nhiêu vectơ khác vectơ - không cùng phương với \(\overrightarrow {MN} \) có điểm đầu và điểm cuối lấy trong các điểm đã cho.
Cách viết nào sau đây là đúng
Cho hàm số \(y = -3{x^2}-2x + 5\). Đồ thị hàm số này có thể được suy ra từ đồ thị hàm số \(y = - 3{x^2}\) bằng cách
Các câu sau đây,có bao nhiêu câu là mệnh đề?
(1) Ở đây đẹp quá!
(2) Phương trình \({x^2} - 3x + 1 = 0\) vô nghiệm
(3) $16$ không là số nguyên tố
(4) Hai phương trình \({x^2} - 4x + 3 = 0\) và \({x^2} - \sqrt {x + 3} + 1 = 0\) có nghiệm chung.
(5) Số \(\pi \) có lớn hơn \(3\) hay không?
(6) Italia vô địch Worldcup $2006$
(7) Hai tam giác bằng nhau khi và chỉ khi chúng có diện tích bằng nhau.
(8) Một tứ giác là hình thoi khi và chỉ khi nó có hai đường chéo vuông góc với nhau.
Cho hình vuông \(ABCD\) cạnh \(a.\) Tính \(\left| {\overrightarrow {AB} - \overrightarrow {DA} } \right|.\)
Cho tam giác \(ABC.\) Có bao nhiêu vectơ khác vectơ - không có điểm đầu và điểm cuối là các đỉnh \(A,{\rm{ }}B,{\rm{ }}C?\)
Lập mệnh đề phủ định của mệnh đề: “ Số \(6\) chia hết cho cả \(2\) và \(3\)”.
Hàm số $y = \left\{ \begin{array}{l}2x \text{ khi } x \ge 1\\x + 1 \text{ khi } x < 1\end{array} \right.$ có đồ thị
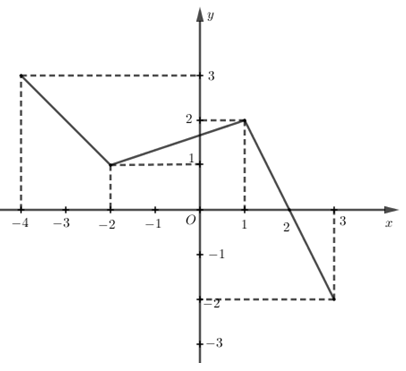
Cho đồ thị hàm số có đồ thị \(\left( C \right)\) (hình vẽ). Tìm tổng giá trị lớn nhất và nhỏ nhất của hàm số trên \(\left[ { - 4;2} \right]\)
Trong các mệnh đề sau, mệnh đề nào sai ?
Tìm $m$ để \(\left( { - 1;1} \right) \subset \left( {m;m + 3} \right)\)
Tìm giá trị thực của tham số \(m\) để ba đường thẳng \(y = 2x\), \(y = - x - 3\) và \(y = mx + 5\) phân biệt và đồng qui.
Viết phương trình của Parabol $(P)$ biết rằng $(P)$ đi qua các điểm $A\left( {0;\,\,2} \right),\,\,B\left( { - 2;\,\,5} \right),\,\,C\left( {3;\,\,8} \right)$
Cho hàm số: \(y = \dfrac{{mx}}{{\sqrt {x - m + 2} - 1}}\) với \(m\) là tham số. Tìm \(m\) để hàm số xác định trên \(\left( {0;1} \right)\)
Cho lục giác đều $ABCDEF$ và $O$ là tâm của nó. Đẳng thức nào dưới đây là đẳng thức sai?
Cho hàm số \(y = 3\left| {x - 2} \right| - \left| {2x - 6} \right|\) có đồ thị \((C)\). Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên với \(x \in \left[ { - 3;4} \right]\)
Trong mặt phẳng tọa độ $Oxy$, cho hình bình hành $ABCD$ có $A\left( {2;{\rm{ }}3} \right)$ và tâm $I\left( { - 1;{\rm{ }}1} \right)$. Biết điểm $M\left( {4;{\rm{ }}9} \right)$ nằm trên đường thẳng $AD$ và điểm $D$ có tung độ gấp đôi hoành độ. Tìm các đỉnh còn lại của hình bình hành?
Cho hàm số \(y = m{x^2} - 2\left( {m - 1} \right)x + 1\left( {m \ne 0} \right)\) có đồ thị \(\left( {{C_m}} \right)\). Tịnh tiến \(\left( {{C_m}} \right)\) qua trái \(1\) đơn vị ta được đồ thị hàm số \(\left( {{C_m}'} \right)\). Giá trị của \(m\) để giao điểm của \(\left( {{C_m}} \right)\) và \(\left( {{C_m}'} \right)\) có hoành độ \(x = \dfrac{1}{4}\) thỏa mãn điều kiện nào dưới đây?