Kết quả:
0/25
Thời gian làm bài: 00:00:00
Tìm tập xác định của hàm số$y = \dfrac{{x - 2}}{{{x^3} + {x^2} - 5x - 2}}$
Cho các mệnh đề:
(1) “\(\sqrt 2 \) là số hữu tỉ”.
(2) “\(5\) không chia hết cho \(3\)”.
(3) “Tam giác có tổng số đo các góc bằng \({180^0}\)”.
(4) “Hình vuông có bốn góc bằng nhau”.
Số mệnh đề có mệnh đề phủ định là mệnh đề đúng là:
Điều kiện nào là điều kiện cần và đủ để \(I\) là trung điểm của đoạn thẳng \(AB\)?
Có bao nhiêu giá trị nguyên của $m$ thuộc đoạn $\left[ {0;\,\,3} \right]$ để hàm số $y = \left( {{m^2} - 1} \right)x$ đồng biến trên $R.$
Kí hiệu nào sau đây dùng để viết đúng mệnh đề \(''\)\(7\) là số tự nhiên khác \(0\)\(''\)?
Cho hàm số:$f(x) = \left\{ \begin{array}{l}\dfrac{x}{{x + 1}},{\rm{ }}x \ge 0\\\dfrac{1}{{x - 1}},{\rm{ }}x < 0\end{array} \right.$. Giá trị $f\left( 0 \right),f\left( 2 \right),f\left( { - 2} \right)$ là
Trên đường thẳng $MN$ lấy điểm $P$ sao cho \(\overrightarrow {MN} = - 3\overrightarrow {MP} \). Điểm $P$ được xác định đúng trong hình vẽ nào sau đây:
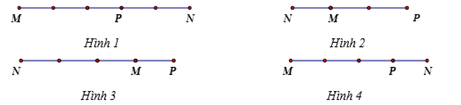
Mệnh đề \(P\) kéo theo \(Q\) kí hiệu là:
Cho tam giác \(ABC\) vuông cân tại \(A\) có \(AB = a\). Tính \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|.\)
Xét ba đường thẳng sau: $2x-y + 1 = 0$;$x + 2y-17 = 0$;$x + 2y-3 = 0$. Chọn kết luận đúng:
Giao điểm của parabol \(\left( P \right)\): \(y = {x^2} + 5x + 4\) với trục hoành:
Cho tam giác \(ABC\) có thể xác định được bao nhiêu vectơ (khác vectơ không) có điểm đầu và điểm cuối là đỉnh\(A\),\(B\), \(C\) ?
Cho các tập hợp \(A = \left\{ {0;2;4;6;8} \right\}\),\(B = \left\{ {3;6;9;12;15} \right\}\) ,\(C = \left\{ {1;2;4;8;16} \right\}\). Mệnh đề nào sau đây đúng?
Cho hai điểm $A\left( {1;0} \right)$ và $B\left( {0; - 2} \right)$. Tọa độ trung điểm của đoạn thẳng $AB$ là:
Trong các khẳng định sau khẳng định nào đúng:
Cho $\overrightarrow a = 3\overrightarrow i - 4\overrightarrow j $ và $\overrightarrow b = \overrightarrow i - \overrightarrow j $. Tìm phát biểu sai:
“Chứng minh rằng \(\sqrt 2 \) là số vô tỉ”. Một học sinh đã lập luận như sau:
Bước 1: Giả sử \(\sqrt 2 \) là số hữu tỉ, thế thì tồn tại các số nguyên dương $m,n$ sao cho \(\sqrt 2 = \dfrac{m}{n}\) (1)
Bước 2: Ta có thể giả định thêm \(\dfrac{m}{n}\) là phân số tối giản.
Từ đó $2{n^2} = {m^2}$ (2).
Suy ra ${m^2}$ chia hết cho $2 \Rightarrow m$ chia hết cho $2 \Rightarrow $ ta có thể viết $m = 2p$.
Nên (2) trở thành ${n^2} = 2{p^2}$ .
Bước 3: Như vậy ta cũng suy ra n chia hết cho $2$ và cũng có thể viết $n = 2q$ .
Và (1) trở thành \(\sqrt 2 = \dfrac{{2p}}{{2q}} = \dfrac{p}{q} \Rightarrow \dfrac{m}{n}\) không phải là phân số tối giản, trái với giả thiết.
Bước 4: Vậy \(\sqrt 2 \) là số vô tỉ.
Lập luận trên đúng tới hết bước nào?
Cho hai tập hợp \(A = \left( {m - 1;5} \right)\,\) và \(B = \left( {3; + \infty } \right)\). Tìm tất cả các giá trị thực của tham số \(m\) để \(A\backslash B = \emptyset \).
Tìm tất cả các giá trị thực của tham số \(m\) để đường thẳng \(d:y = \left( {3m + 2} \right)x - 7m - 1\) vuông góc với đường \(\Delta :y = 2x - 1.\)
Viết phương trình của Parabol $(P)$ biết rằng $(P)$ đi qua các điểm $A\left( {0;\,\,2} \right),\,\,B\left( { - 2;\,\,5} \right),\,\,C\left( {3;\,\,8} \right)$
Tìm \(m\) để đồ thị hàm số sau nhận gốc tọa độ $O$ làm tâm đối xứng \(y = {x^3} - ({m^2} - 9){x^2} + (m + 3)x + m - 3\).
Gọi $G$ là trọng tâm tam giác vuông $ABC\;$ với cạnh huyền $BC = 12$. Vectơ $\overrightarrow {GB} - \overrightarrow {CG} $ có độ dài bằng bao nhiêu?
Trong mặt phẳng $Oxy$, cho tam giác \(MNP\) có \(M\left( {1;{\rm{ }} - 1} \right)\), \(N\left( {5;{\rm{ }} - 3} \right)\) và \(P\) là điểm thuộc trục \(Oy\), trọng tâm \(G\) của tam giác \(MNP\) nằm trên trục \(Ox\). Tọa độ điểm \(P\) là
Xét sự biến thiên của hàm số \(y = \sqrt {4x + 5} + \sqrt {x - 1} \) trên tập xác định của nó. Áp dụng tìm số nghiệm của phương trình \(\sqrt {4x + 5} + \sqrt {x - 1} = 3\)
Cho hàm số \(y = m{x^2} - 2\left( {m - 1} \right)x + 1\left( {m \ne 0} \right)\) có đồ thị \(\left( {{C_m}} \right)\). Tịnh tiến \(\left( {{C_m}} \right)\) qua trái \(1\) đơn vị ta được đồ thị hàm số \(\left( {{C_m}'} \right)\). Giá trị của \(m\) để giao điểm của \(\left( {{C_m}} \right)\) và \(\left( {{C_m}'} \right)\) có hoành độ \(x = \dfrac{1}{4}\) thỏa mãn điều kiện nào dưới đây?

