Kết quả:
0/12
Thời gian làm bài: 00:00:00
Hàm số nào sau đây nghịch biến trong khoảng \(\left( { - \infty ;\,0} \right)\)?
Đường thẳng nào trong các đường thẳng sau đây là trục đối xứng của parabol \(y = - 2{x^2} + 5x + 3.\)
Tìm tất cả các giá trị thực của \(m\) để hai đường thẳng \(d:y = mx - 3\) và \(\Delta :y + x = m\) cắt nhau tại một điểm nằm trên trục hoành.
Câu nào sau đây đúng?
Xét tính đồng biến, nghịch biến của hàm số \(f\left( x \right) = \dfrac{{x - 3}}{{x + 5}}\) trên khoảng \(\left( { - \infty ; - 5} \right)\) và trên khoảng \(\left( { - 5; + \infty } \right)\). Khẳng định nào sau đây đúng?
Tìm \(m\) để hàm số \(y = \left( {2m + 1} \right)x + m - 3\) đồng biến trên \(\mathbb{R}.\)
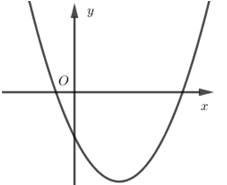
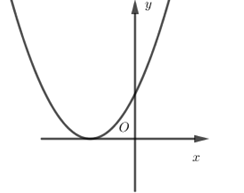
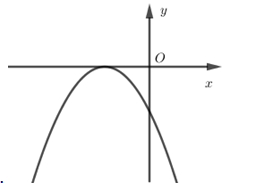
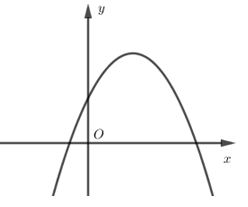
Nếu hàm số $y = a{x^2} + bx + c$ có $a < 0,b > 0$ và $c > 0$ thì đồ thị của nó có dạng:
Cho điểm \(M\left( {m - 1;\,\,2m + 1} \right)\), điểm \(M\) luôn nằm trên đường thẳng cố đinh nào dưới đây ?
Tìm $m$ để ba đường thẳng $y = 2x - 3\,\,\left( {{d_1}} \right);\,\,\,y = x - 1\,\,\left( {{d_2}} \right);\,\,\,y = \left( {m - 1} \right)x + 2\,\,\,\,\left( {{d_3}} \right)$ đồng quy.
Cho hai điểm A, B thõa mãn hệ phương trình \(\left\{ \begin{array}{l}{x_A} + {y_A} - 1 = 0\\{x_B} + {y_B} - 1 = 0\end{array} \right.\). Tìm m đề đường thẳng AB cắt đường thẳng \(y = x + m\) tại điểm C có tọa độ thỏa mãn \({y_C} = x_C^2\).
Cho hàm số $y = f(x) = ax^2 + bx +c.$ Rút gọn biểu thức $f(x + 3) – 3f(x + 2) + 3f(x + 1) $ ta được:
Tìm tọa độ giao điểm của hai parabol: \(y = \dfrac{1}{2}{x^2} - x\) và \(y = - 2{x^2} + x + \dfrac{1}{2}\) là: