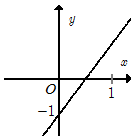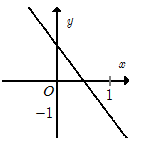Kết quả:
0/25
Thời gian làm bài: 00:00:00
Đỉnh của parabol \(\left( P \right):y = 3{x^2} - 2x + 1\) là
Tìm các giá trị của m để hàm số $y = {x^2} + mx + 5$ luôn đồng biến trên $\left( {1;\,\, + \infty } \right)$.
Có bao nhiêu giá trị nguyên của $m$ thuộc đoạn $\left[ {0;\,\,3} \right]$ để hàm số $y = \left( {{m^2} - 1} \right)x$ đồng biến trên $R.$
Cho hàm số \(y = f\left( x \right) = \left| { - 5x} \right|\). Khẳng định nào sau đây là sai?
Cho hàm số \(y = ax + b\) có đồ thị là hình bên. Giá trị của $a$ và $b$ là:
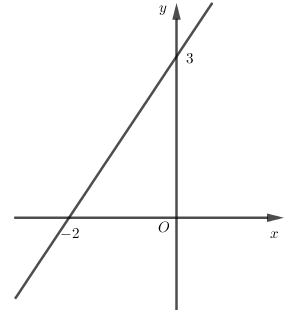
Đồ thị sau đây biểu diễn hàm số nào?
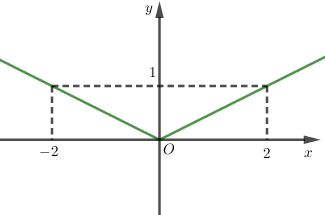
Trong các hàm số nào sau đây, hàm số nào là hàm số chẵn?
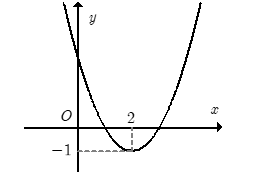
Cho hàm số \(y = a{x^2} + bx + c\) có đồ thị \(\left( P \right)\) như hình vẽ.
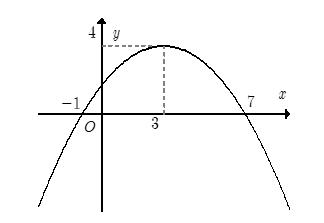
Khẳng định nào sau đây là sai?
Cho hai hàm số $f\left( x \right)$ và $g\left( x \right)$ cùng đồng biến trên khoảng $\left( {a;b} \right)$. Có thể kết luận gì về chiều biến thiên của hàm số $y = f\left( x \right) + g\left( x \right)$ trên khoảng $\left( {a;b} \right)$?
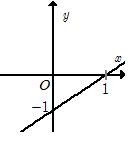
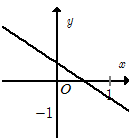
Hàm số \(y = 2x - 1\) có đồ thị là hình nào trong bốn hình sau?
Tìm tất cả các giá trị thực của \(m\) để đường thẳng \(y = {m^2}x + 2\) cắt đường thẳng \(y = 4x + 3\).
Đường thẳng nào trong các đường thẳng sau đây là trục đối xứng của parabol \(y = - 2{x^2} + 5x + 3.\)
Cho hàm số $y = 2\left( {m - 1} \right)x - {m^2} - 3\,\,\,\left( d \right)$. Tìm tất cả các giá trị của $m$ để $(d)$ cắt trục hoành tại một điểm có hoành độ ${x_0}$ thỏa mãn ${x_0} < 2$.
Xác định Parabol $\left( P \right):\,\,y = a{x^2} + bx + 3$ biết rằng Parabol có đỉnh $I\left( {3;\,\, - 2} \right)$.
Tìm tất cả các giá trị thực của tham số \(m\) để hàm số \(y = - {x^2} + \left( {m - 1} \right)x + 2\) nghịch biến trên khoảng \(\left( {1;2} \right)\).
Biết rằng đường thẳng $d:y = ax + b$ đi qua điểm $M\left( {4;\,\, - 3} \right)$ và song song với đường thẳng $y = - \dfrac{2}{3}x + 1$. Tính giá trị biểu thức ${a^2} + {b^3}$.
Gọi \(S\) là tập hợp tất cả các giá trị thực của tham số \(m\) để giá trị nhỏ nhất của hàm số \(y = f\left( x \right) = 4{x^2} - 4mx + {m^2} - 2m\) trên đoạn \(\left[ { - 2;0} \right]\) bằng \(3.\) Tính tổng \(T\) các phần tử của \(S.\)
Tìm tọa độ giao điểm của hai parabol: \(y = \dfrac{1}{2}{x^2} - x\) và \(y = - 2{x^2} + x + \dfrac{1}{2}\) là:
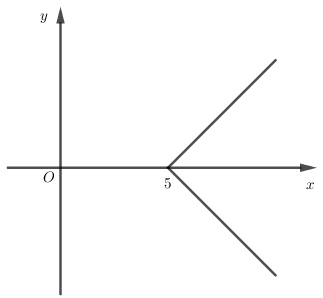
Hàm số $y = \left| {x - 5} \right|$ có đồ thị nào trong các đồ thị sau đây?
Tìm điểm $A$ cố định mà họ đồ thị hàm số $y = {x^2} + \left( {2 - m} \right)x + 3m\,\,\left( {{P_m}} \right)$ luôn đi qua.
Tìm giá trị của m để đồ thị hàm số $y = {x^2} - 2x + m - 1$ cắt trục hoành tại hai điểm phân biệt có hoành độ dương.
Tìm giá trị nhỏ nhất của hàm số $f\left( x \right)$ biết rằng $f\left( {x + 2} \right) = {x^2} - 3x + 2$ trên $\mathbb{R}$
Cho hàm số \(f\left( x \right) = a{x^2} + bx + c\) đồ thị như hình. Hỏi với những giá trị nào của tham số thực \(m\) thì phương trình \(\left| {f\left( x \right)} \right| = m\) có đúng \(4\) nghiệm phân biệt.
Tìm tất cả các giá trị của $m$ để phương trình $\left| {x + 1} \right| + \left| {x - 1} \right| = {m^2} - 2$ có hai nghiệm phân biệt.
Tìm các giá trị của tham số m để phương trình $\dfrac{1}{2}{x^2} - 4\left| x \right| + 3 = {m^2}$ có 3 nghiệm thực phân biệt.