Câu hỏi:
2 năm trước
Gọi \(S\) là tập hợp tất cả các giá trị thực của tham số \(m\) để giá trị nhỏ nhất của hàm số \(y = f\left( x \right) = 4{x^2} - 4mx + {m^2} - 2m\) trên đoạn \(\left[ { - 2;0} \right]\) bằng \(3.\) Tính tổng \(T\) các phần tử của \(S.\)
Trả lời bởi giáo viên
Đáp án đúng: d
Parabol có hệ số theo \({x^2}\) là \(4 > 0\) nên bề lõm hướng lên. Hoành độ đỉnh \({x_I} = \dfrac{m}{2}\).
Nếu \(\dfrac{m}{2} < - 2 \Leftrightarrow m < - 4\) thì \({x_I} < - 2 < 0\,\). Suy ra \(f\left( x \right)\) đồng biến trên đoạn \(\left[ { - 2;0} \right]\).
Do đó \(\mathop {\min }\limits_{\left[ { - 2;0} \right]} f\left( x \right) = f\left( { - 2} \right) = {m^2} + 6m + 16\).
Theo yêu cầu bài toán: \({m^2} + 6m + 16 = 3\) (vô nghiệm).
Nếu \( - 2 \le \dfrac{m}{2} \le 0 \Leftrightarrow - 4 \le m \le 0\) thì \({x_I} \in \left[ {0;2} \right]\).
Suy ra \(f\left( x \right)\) đạt giá trị nhỏ nhất tại đỉnh. Do đó \(\mathop {\min }\limits_{\left[ { - 2;0} \right]} f\left( x \right) = f\left( {\dfrac{m}{2}} \right) = - 2m\).
Theo yêu cầu bài toán \( - 2m = 3 \Leftrightarrow m = - \dfrac{3}{2}\) (thỏa mãn \( - 4 \le m \le 0\)).
Nếu \(\dfrac{m}{2} > 0 \Leftrightarrow m > 0\) thì \({x_I} > 0 > - 2\). Suy ra \(f\left( x \right)\) nghịch biến trên đoạn \(\left[ { - 2;0} \right]\).
Do đó \(\mathop {\min }\limits_{\left[ { - 2;0} \right]} f\left( x \right) = f\left( 0 \right) = {m^2} - 2m.\)
Theo yêu cầu bài toán: \({m^2} - 2m = 3 \Leftrightarrow \left[ \begin{array}{l}m = - 1\,\,\left( {loại} \right)\\m = 3\,\,\,\left( {thỏa mãn} \right)\end{array} \right..\)
Bảng biến thiên:
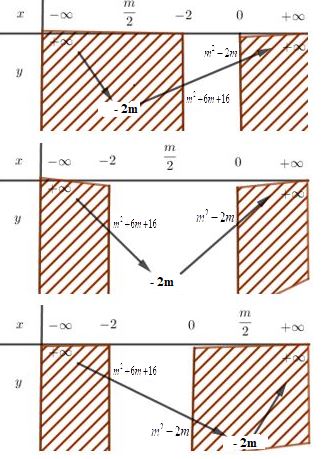
Hướng dẫn giải:
- Tìm hoành độ đỉnh \({x_I}\).
- Xét các trường hợp \({x_I} < - 2\), \( - 2 \le {x_I} \le 0\) và \({x_I} > 0\) để tìm GTNN của hàm số trong các trường hợp đó.
Câu hỏi khác
- Đề kiểm tra 1 tiết chương 2: Hàm số bậc nhất và bậc hai - đề số 2 Toán 10 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 2: Hàm số bậc nhất và bậc hai - đề số 3 Toán 10 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 2: Hàm số bậc nhất và bậc hai - đề số 1 Toán 10 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 2: Hàm số bậc nhất và bậc hai - đề số 2 Toán 10 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 2: Hàm số bậc nhất và bậc hai - đề số 1 Toán 10 có lời giải chi tiết
