Tìm tất cả các giá trị của $m$ để phương trình $\left| {x + 1} \right| + \left| {x - 1} \right| = {m^2} - 2$ có hai nghiệm phân biệt.
Trả lời bởi giáo viên
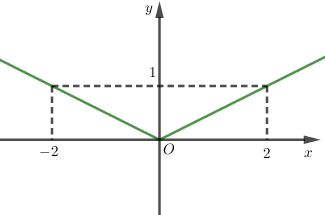
Ta có $y = \left| {x + 1} \right| + \left| {x - 1} \right| = \left\{ \begin{array}{l} - 2x\,\,\,\left( {x < - 1} \right)\\2\,\,\,\,\,\,\left( { - 1 \le x \le 1} \right)\\2x\,\,\,\,\left( {x \ge 1} \right)\end{array} \right.$ và có đồ thị chính là phần đường thẳng màu xanh như sau:
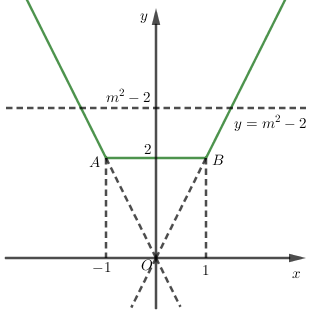
Đường thẳng $d:\,\,y = {m^2} - 2$ song song với trục hoành.
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số $y = \left\{ \begin{array}{l} - 2x\,\,\,\left( {x < - 1} \right)\\2\,\,\,\,\,\,\left( { - 1 \le x \le 1} \right)\\2x\,\,\,\,\left( {x \ge 1} \right)\end{array} \right.$ và đường thẳng $d:\,\,y = {m^2} - 2$.
Nhìn vào đồ thị ta thấy đường thẳng $y=m^2-2$ chỉ cắt đồ thị hàm số (đường màu xanh) tại $2$ điểm phân biệt khi $m^2-2>2$
Hay phương trình đã cho có hai nghiệm phân biệt khi ${m^2} - 2 > 2 \Rightarrow {m^2} > 4 \Leftrightarrow \left[ \begin{array}{l}m < - 2\\m > 2\end{array} \right.$.
Hướng dẫn giải:
- Vẽ đồ thị hàm số $y = \left| {x + 1} \right| + \left| {x - 1} \right|$.
- Nhận xét số nghiệm của phương trình cũng là số giao điểm của đường thẳng \(y = {m^2} - 2\) với đồ thị hàm số vừa vẽ.
Giải thích thêm:
Ở lời giải trên, ta không lấy trường hợp $y=2$ vì đường thẳng $y=2$ cắt đồ thị hàm số đã cho tại vô số điểm $x \in [-1;1]$ nên không thỏa mãn bài toán.
Do đó, $m^2-2>2$