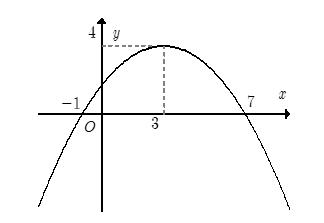
Cho hàm số $y = a{x^2} + bx + c$ có đồ thị $\left( P \right)$ như hình vẽ.
Khẳng định nào sau đây là sai?

Hàm số đồng biến trên khoảng $\left( { - \infty ;3} \right)$.

$\left( P \right)$ có đỉnh là $I\left( {3;4} \right).$

$\left( P \right)$ cắt trục tung tại điểm có tung độ bằng $1.$

$\left( P \right)$ cắt trục hoành tại hai điểm phân biệt.

Xem đáp án

54 lượt xem

Đề kiểm tra 1 tiết chương 2: Hàm số bậc nhất và bậc hai - Đề số 2 - MÔN TOÁN - Lớp 10. Thi ngay

Trả lời bởi giáo viên

Đáp án đúng: c

Đồ thị hàm số đi lên trên khoảng $\left( { - \infty ;3} \right)$ nên đồng biến trên khoảng đó. Do đó A đúng.

Dựa vào đồ thị ta thấy $\left( P \right)$ có đỉnh có tọa độ $\left( {3;4} \right)$. Do đó B đúng.

$\left( P \right)$ cắt trục hoành tại hai điểm phân biệt có hoành độ $ - 1$ và $7$. Do đó D đúng.

Dùng phương pháp loại trừ thì C là đáp án sai.

Hướng dẫn giải:

Quan sát đồ thị và nhận xét.

Giải thích thêm:

Cách giải tự luận.

Gọi parabol cần tìm là $\left( P \right):y = a{x^2} + bx + c$. Do bề lõm quay xuống nên $a < 0$. Vì $\left( P \right)$ cắt trục hoành tại hai điểm $\left( { - 1;0} \right)$ và $\left( {7;0} \right)$ nên $\left\{ \begin{array}{l}a - b + c = 0\\49a + 7b + c = 0\end{array} \right.$.

Mặt khác $\left( P \right)$ có trục đối xứng $x = 3 \to - \dfrac{b}{{2a}} = 3 \Leftrightarrow - b = 6a$ và đi qua điểm $\left( {3;4} \right)$ nên $9a + 3a + c = 4.$

Kết hợp các điều kiện ta tìm được $I\left( { - \dfrac{1}{3}; - \dfrac{2}{3}} \right)$.

Vậy $y = - \dfrac{1}{4}{x^2} + \dfrac{3}{2}x + \dfrac{7}{4}$$ \Rightarrow \left( P \right) \cap Oy = \left( {0;\dfrac{7}{4}} \right)$