Kết quả:
0/25
Thời gian làm bài: 00:00:00
Cho bất phương trình\( - 2x + \sqrt 3 y + \sqrt 2 \le 0\) có tập nghiệm là \(S\). Khẳng định nào sau đây là khẳng định đúng?
Tập hợp nào dưới đây chứa phần tử không là nghiệm của bất phương trình $\sqrt 2 {x^2} - \left( {\sqrt 2 + 1} \right)x + 1 < 0$?
Điều kiện của \(x\) để biểu thức \(B = \left| {x - 2} \right| + \left| {x - 3} \right|\) đạt giá trị nhỏ nhất là
Các giá trị $m$ để tam thức $f(x) = {x^2} - (m + 2)x + 8m + 1$ đổi dấu 2 lần là
Tìm giá trị lớn nhất \(M\) của hàm số \(f\left( x \right) = \dfrac{x}{{{x^2} + 4}}\) với \(x > 0.\)
Tìm tập xác định \({\rm{D}}\) của hàm số \(y = \sqrt {{x^2} + x - 6} + \dfrac{1}{{\sqrt {x + 4} }}.\)
Cho \(\dfrac{1}{a} < \dfrac{1}{b}\) và \(ab > 0\). So sánh \(a\) và \(b\).
Tìm điều kiện xác định của bất phương trình $x + \dfrac{{x - 1}}{{\sqrt {x + 5} }} > 2 - \sqrt {4 - x} .$
Cho biểu thức \(f\left( x \right) = x\left( {x - 2} \right)\left( {3 - x} \right).\) Tập hợp tất cả các giá trị của \(x\) thỏa mãn bất phương trình \(f\left( x \right) < 0\) là
Cho biểu thức \(f\left( x \right) = \dfrac{1}{{3x - 6}}.\) Tập hợp tất cả các giá trị của \(x\) để \(f\left( x \right) \le 0\) là
Tìm giá trị nhỏ nhất $m$ của hàm số $f\left( x \right) = \sqrt {7 - 2x} + \sqrt {3x + 4} .$
Tìm tất cả các giá trị thực của tham số \(m\) để hàm số \(y = \sqrt {x - m} - \sqrt {6 - 2x} \) có tập xác định là rỗng.
Tìm tất cả các giá trị thực của tham số \(m\) để bất phương trình \({m^2}\left( {x - 2} \right) - mx + x + 5 < 0\) nghiệm đúng với mọi \(x \in \left[ { - 2018;2} \right]\).
Cho biểu thức \(f\left( x \right) = \dfrac{{x\left( {x - 3} \right)}}{{\left( {x - 5} \right)\left( {1 - x} \right)}}.\) Tập hợp tất cả các giá trị của \(x\) thỏa mãn bất phương trình \(f\left( x \right) \ge 0\) là
Bất phương trình $\dfrac{{x + 4}}{{{x^2} - 9}} - \dfrac{2}{{x + 3}} < \dfrac{{4x}}{{3x - {x^2}}}$ có nghiệm nguyên lớn nhất là
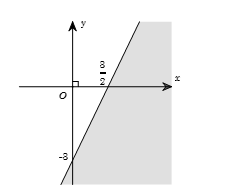
Phần tô đậm trong hình vẽ sau, biểu diễn tập nghiệm của bất phương trình nào trong các bất phương trình sau?
Phương trình \({x^2} - \left( {m + 1} \right)x + 1 = 0\) vô nghiệm khi và chỉ khi
Tập nghiệm của hệ bất phương trình $\left\{ \begin{array}{l}{x^2} - 7x + 6 < 0\,\,\left( 1 \right)\\\left| {2x - 1} \right| < 3\,\,\left( 2 \right)\end{array} \right.$ là:
Bất phương trình $\dfrac{{2{x^2} - x - 1}}{{\left| {x + 1} \right| - 2x}} \le - 2{x^2} + x + 1$ có bao nhiêu nghiệm nguyên?
Cho các số thực \(x,\,\,y\) thỏa mãn \(x - 2y + 2 = 2\left( {\sqrt {x - 1} + \sqrt {3 - 2y} } \right)\). Gọi \(M,\,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(S = x - 2y\). Tính \(M + m\).
Một nhà máy sản xuất, sử dụng ba loại máy đặc chủng để sản xuất sản phẩm \(A\) và sản phẩm \(B\) trong một chu trình sản xuất. Để sản xuất một tấn sản phẩm \(A\) lãi \(4\) triệu đồng người ta sử dụng máy \(I\) trong \(1\) giờ, máy \(II\) trong \(2\) giờ và máy \(III\) trong \(3\) giờ. Để sản xuất ra một tấn sản phẩm \(B\) lãi được \(3\) triệu đồng người ta sử dụng máy \(I\) trong \(6\) giờ, máy \(II\) trong \(3\) giờ và máy \(III\) trong \(2\) giờ. Biết rằng máy \(I\) chỉ hoạt động không quá \(36\) giờ, máy hai hoạt động không quá \(23\) giờ và máy \(III\) hoạt động không quá \(27\) giờ. Hãy lập kế hoạch sản xuất cho nhà máy để tiền lãi được nhiều nhất.
Tìm tất cả các giá trị của tham số \(m\) để bất phương trình \(mx + 4 > 0\) nghiệm đúng với mọi \(\left| x \right| < 8\).

